题目内容
对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数y=f（x）的导数，f′′（x）是f′（x）的导数，若方程f′′（x）有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．设函数f（x）
x3-
x2+3x-
，请你根据这一发现，计算f（
）+f（
）+f（
）+…+f（
）= ．
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 2014 |
| 2015 |
考点：类比推理
专题：计算题,推理和证明
分析：由题意可推出（
，1）为f（x）的对称中心，从而可得f（
）+f（
）=2f（
）=2，从而求f（
）+f（
）+f（
）+…+f（
）=2014的值．
| 1 |
| 2 |
| 1 |
| 2015 |
| 2014 |
| 2015 |
| 1 |
| 2 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 2014 |
| 2015 |
解答：
解：f′（x）=x2-x+3，
由f′′（x）=2x-1=0得x0=
，
f（x0）=1，
则（
，1）为f（x）的对称中心，由于
+
=1，
则f（
）+f（
）=2f（
）=2，
则f（
）+f（
）+f（
）+…+f（
）=2014．
故答案为：2014．
由f′′（x）=2x-1=0得x0=
| 1 |
| 2 |
f（x0）=1，
则（
| 1 |
| 2 |
| 1 |
| 2015 |
| 2014 |
| 2015 |
则f（
| 1 |
| 2015 |
| 2014 |
| 2015 |
| 1 |
| 2 |
则f（
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 2014 |
| 2015 |
故答案为：2014．
点评：本题考查了类比推理的应用，属于基础题．
练习册系列答案
相关题目
如图，平面正六边形ABCDEF中，不能和
组成平面向量基底的是（ ）
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
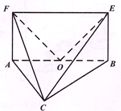如图，平面ABEF⊥平面ABC，四边形ABEF为矩形，AC=BC，O为AB的中点，OF⊥EC．