题目内容
已知向量
与
满足|
|=4，|
|=2，|
+
|=2
．
（1）求
•
（2）求|3
-4
|
（3）求（
-2
）•（
+
）．
| a |
| b |
| a |
| b |
| a |
| b |
| 3 |
（1）求
| a |
| b |
（2）求|3
| a |
| b |
（3）求（
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算,向量的模
专题：计算题,平面向量及应用
分析：（1）运用向量的平方即为模的平方，化简即可得到；
（2）运用向量模的平方即为向量的平方，结合（1），计算即可得到；
（3）由向量的平方即为模的平方，结合（1）的结论，即可得到所求值．
（2）运用向量模的平方即为向量的平方，结合（1），计算即可得到；
（3）由向量的平方即为模的平方，结合（1）的结论，即可得到所求值．
解答：
解：（1）|
|=4，|
|=2，|
+
|=2
，
则（
+
）2=12，即有
2+
2+2
•
=12，
即16+4+2
•
=12，解得，
•
=-4；
（2）|3
-4
|2=9
2+16
2-24
•
=9×16+16×4-24×（-4）=16×19，
则有|3
-4
|=4
；
（3）（
-2
）•（
+
）=
2-2
2-
•
=16-2×4-（-4）=12．
| a |
| b |
| a |
| b |
| 3 |
则（
| a |
| b |
| a |
| b |
| a |
| b |
即16+4+2
| a |
| b |
| a |
| b |
（2）|3
| a |
| b |
| a |
| b |
| a |
| b |
=9×16+16×4-24×（-4）=16×19，
则有|3
| a |
| b |
| 19 |
（3）（
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
=16-2×4-（-4）=12．
点评：本题考查平面向量的数量积的坐标表示和性质，考查向量的平方即为模的平方，考查运算能力，属于基础题．
练习册系列答案
相关题目
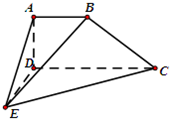如图，在四棱锥E-ABCD中，AB∥CD，CD=2AB，