题目内容

设{an}是正项数列，a1=2，an+12-an2=2，则an=
 
．
考点：数列递推式
专题：计算题,等差数列与等比数列
分析：由已知条件推导出{an2}是首项为4，公差为2的等差数列，由此能求出an．
解答： 解：∵a1=2，an+12-an2=2，
∴{an2}是首项为4，公差为2的等差数列，
∴an2=4+2（n-1）=2n+2，
∵{an}是正项数列，
∴an=
2n+2
．
故答案为：
2n+2
．
点评：本题考查数列的前n项和的求法，解题时要认真审题，注意等差数列的性质的灵活运用．
练习册系列答案
相关题目
如图，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则几何体的表面积为（　　）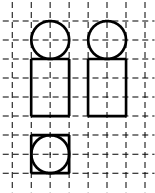
A、32+4π
B、24+4π
C、12+
4π
3
D、24+
4π
3
已知双曲线
x2
a2
-
y2
b2
=1（b＞a＞0），直线l过点A（a，0）和B（0，b），若原点O到直线l的距离为
3
c
4
（c为双曲线的半焦距），则双曲线的离心率为（　　）
A、
2
3
3
或2
B、
2
C、
2
3
3
D、2
计算：
（1）
5
6
a
1
3
•b-2（-3a-
1
2
b-1）÷(4a
2
3
•b-2)
1
2
+（
3
6a9
）4（
6
3a9
）；
（2）0.027 -
1
3
-（-
1
7
）-2+256 
3
4
-（
3
5
）0+（
9
4
）-0.5+
5-2
6
；
（3）2（lg
2
）2+lg
2
•lg5+
(lg
2
)2-lg2+1
．
函数y=
1
2
x2-ax-
27
2x2
在（0，+∞）上是增函数，则实数a的最大值为（　　）
A、3B、4C、5D、6
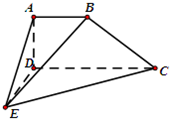如图，在四棱锥E-ABCD中，AB∥CD，CD=2AB，
（Ⅰ）在线段CE上找一点M，使得BM∥平面ADE，并给予证明．
（Ⅱ）若平面ADE∩平面BCE=l，试证明：l∥BM．
求过原点作曲线C：y=x3-3x2+2x-1的切线方程．
对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数y=f（x）的导数，f′′（x）是f′（x）的导数，若方程f′′（x）有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．设函数f（x）
1
3
x3-
1
2
x2+3x-
5
12
，请你根据这一发现，计算f（
1
2015
）+f（
2
2015
）+f（
3
2015
）+…+f（
2014
2015
）=
 
．
已知f（x）=x-k2+k+2（k∈z）满足f（2）＜f（3）．
①求k及f（x）；
②判断是否存在q＞0使g（x）=1-qf（x）+（2q-1）x在[-1，2]上的值域为[-4，
17
8
]，若存在求出q；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网