题目内容
已知点A1(-2,0),A2(2,0),过点A1的直线l1与过点A2的直线l2相交于点M,设直线l1斜率为k1,直线l2斜率为k2,且k1k2=-
.
(1)求直线l1与l2的交点M的轨迹方程;
(2)已知F2(1,0),设直线l:y=kx+m与(1)中的轨迹M交于P、Q两点,直线F2P、F2Q的倾斜角分别为α、β,且α+β=π,求证:直线l过定点,并求该定点的坐标.
| 3 |
| 4 |
(1)求直线l1与l2的交点M的轨迹方程;
(2)已知F2(1,0),设直线l:y=kx+m与(1)中的轨迹M交于P、Q两点,直线F2P、F2Q的倾斜角分别为α、β,且α+β=π,求证:直线l过定点,并求该定点的坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设点M(x,y),由已知条件推导出k1•k2=
•
=-
,由此能求出点M的轨迹方程.
(2)联立
,得(3+4k2)x2+8kmx+4m2-12=0,由此利用韦达定理结合已知条件求出直线PQ的方程为y=k(x-4).由此能证明直线PQ过定点(4,0).
| y |
| x+2 |
| y |
| x-2 |
| 3 |
| 4 |
(2)联立
|
解答:
(1)解:设点M(x,y),
∵点A1(-2,0),A2(2,0),
过点A1的直线l1与过点A2的直线l2相交于点M,
直线l1斜率为k1,直线l2斜率为k2,且k1k2=-
,
∴k1=
,k2=
,
由k1•k2=
•
=-
,整理得
+
=1
∵由题意点M不与A1(-2,0),A2(2,0)重合,
∴点A1(-2,0),A2(2,0)不在轨迹上,
∴点M的轨迹方程为
+
=1(x≠±2).
(2)证明:由题意知,直线l的斜率存在且不为零,
联立方程
,消y,得(3+4k2)x2+8kmx+4m2-12=0,
设P(x1,y1),Q(x2,y2),则
,
且kF1P=
,kF1Q=
,
由已知α+β=π,得kF1P+kF1Q=0,
∴
+
=0,
化简,得2kx1x2+(m-k)(x1+x2)-2m=0,
∴2k•
-
-2m=0,
整理,得:m=-4k,
∴直线PQ的方程为y=k(x-4).
∴直线PQ过定点,该定点坐标为(4,0).
∵点A1(-2,0),A2(2,0),
过点A1的直线l1与过点A2的直线l2相交于点M,
直线l1斜率为k1,直线l2斜率为k2,且k1k2=-
| 3 |
| 4 |
∴k1=
| y |
| x+2 |
| y |
| x-2 |
由k1•k2=
| y |
| x+2 |
| y |
| x-2 |
| 3 |
| 4 |
| x2 |
| 4 |
| y2 |
| 3 |
∵由题意点M不与A1(-2,0),A2(2,0)重合,
∴点A1(-2,0),A2(2,0)不在轨迹上,
∴点M的轨迹方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)证明:由题意知,直线l的斜率存在且不为零,
联立方程
|
设P(x1,y1),Q(x2,y2),则
|
且kF1P=
| kx1+m |
| x1-1 |
| kx2+m |
| x2-1 |
由已知α+β=π,得kF1P+kF1Q=0,
∴
| kx1+m |
| x1-1 |
| kx2+m |
| x2-1 |
化简,得2kx1x2+(m-k)(x1+x2)-2m=0,
∴2k•
| 4m2-12 |
| 3+4k2 |
| 8mk(m-k) |
| 3+4k2 |
整理,得:m=-4k,
∴直线PQ的方程为y=k(x-4).
∴直线PQ过定点,该定点坐标为(4,0).
点评:本题考查点的轨迹方程的求法,考查直线过定点的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
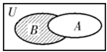 已知全集U={x∈N|0<x≤8},集合A={1,2,4,5},B={3,5,7,8},则图中阴影部分所表示的集合是( )
已知全集U={x∈N|0<x≤8},集合A={1,2,4,5},B={3,5,7,8},则图中阴影部分所表示的集合是( )| A、{1,2,4} |
| B、{3,7,8} |
| C、{1,2,4,6} |
| D、{3,6,7,8} |
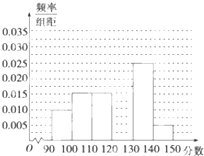 某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: