题目内容
设等差数列{an}的公差为d，前n项和为Sn，已知S3=a5，S5=25．
（1）求数列{an}的通项公式；
（2）若p，q为互不相等的正整数，且等差数列{bn}满足b ap=p，b aq=q，求数列{bn}的前n项和Tn．
（1）求数列{an}的通项公式；
（2）若p，q为互不相等的正整数，且等差数列{bn}满足b ap=p，b aq=q，求数列{bn}的前n项和Tn．
考点：数列的求和,等差数列的性质
专题：等差数列与等比数列
分析：（1）根据等差数列的通项公式，建立方程组求出首项和公差，即可求数列{an}的通项公式；
（2）根据等差数列的通项公式根据b ap=p，b aq=q，即可得到数列{bn}的前n项和Tn．
（2）根据等差数列的通项公式根据b ap=p，b aq=q，即可得到数列{bn}的前n项和Tn．
解答：
解：（1）由已知，得
，解得a1=1，d=2，
∴an=2n-1．
（2）∵p，q为正整数，由（1）得ap=2p-1，ap=2q-1，
进一步由已知，得b2p-1=p，b2q-1=q，
∵{bn}是等差数列，p≠q，
∴{bn}的公差d=
=
，
由b2p-1=b1+(2p-2)×
=p，
得b1=1．
∴Tn=nb1+
d=
．
|
∴an=2n-1．
（2）∵p，q为正整数，由（1）得ap=2p-1，ap=2q-1，
进一步由已知，得b2p-1=p，b2q-1=q，
∵{bn}是等差数列，p≠q，
∴{bn}的公差d=
| q-p |
| 2q-2p |
| 1 |
| 2 |
由b2p-1=b1+(2p-2)×
| 1 |
| 2 |
得b1=1．
∴Tn=nb1+
| n(n-1) |
| 2 |
| n2+3n |
| 4 |
点评：本题主要考查等差数列的通项公式以及等差数列的前n项和的计算，考查学生的计算能力．
练习册系列答案
相关题目
平面内有n个圆，其中每两个圆都相交于两点，且每三个圆都不共点，用f（n）表示这n个圆把平面分割的区域数，那么f（n+1）与f（n）之间的关系为（ ）
| A、f（n+1）=f（n）+n |
| B、f（n+1）=f（n）+2n |
| C、f（n+1）=f（n）+n+1 |
| D、f（n+1）=f（n）+n-1 |
在空间直坐标系中，点P在x轴上，它到P1（0，
，3）的距离为2
，则点P的坐标为（ ）
| 2 |
| 3 |
| A、（0，1，0）或（0，-1，0） |
| B、（1，0，0） |
| C、（1，0，0）或（-1，0，0） |
| D、（0，1，0）或（0，0，1） |
“sinA=
”是“A=45°”的（ ）
| ||
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
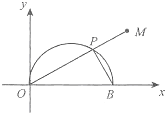在直角坐标xoy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=2cosθ，如图，曲线C与x轴交于O，B两点，P是曲线C在x轴上方图象上任意一点，连结OP并延长至M，使PM=PB，当P变化时，求动点M的轨迹的长度．