题目内容
在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+S2=12,q=
(Ⅰ)求an与bn;
(Ⅱ)设数列{cn}满足cn=
,求{cn}的前n项和Tn.
| S2 |
| b2 |
(Ⅰ)求an与bn;
(Ⅱ)设数列{cn}满足cn=
| 1 |
| Sn |
考点:等差数列与等比数列的综合
专题:综合题,等差数列与等比数列
分析:(Ⅰ)利用待定系数法,建立方程组,求出d,q,即可求an与bn;
(Ⅱ)确定数列{cn}的通项,利用裂项法,可求{cn}的前n项和Tn.
(Ⅱ)确定数列{cn}的通项,利用裂项法,可求{cn}的前n项和Tn.
解答:
解:(Ⅰ)设{an}的公差为d,
因为
所以
…(2分)
解得 q=3或q=-4(舍),d=3. …(4分)
故an=3+3(n-1)=3n,bn=3n-1. …(6分)
(Ⅱ)∵Sn=
,
∴cn=
=
=
(
-
),
∴Tn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)=
.
因为
|
|
解得 q=3或q=-4(舍),d=3. …(4分)
故an=3+3(n-1)=3n,bn=3n-1. …(6分)
(Ⅱ)∵Sn=
| n(3+3n) |
| 2 |
∴cn=
| 1 |
| Sn |
| 2 |
| n(3+3n) |
| 2 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 2 |
| 3 |
| 1 |
| n+1 |
| 2n |
| 3(n+1) |
点评:本题考查等差数列与等比数列的综合,考查数列的通项与求和,考查裂项法的运用,属于中档题.

练习册系列答案
相关题目
已知A、B、C是直线l上不同的三个点,点O不在直线l上,则使等式x2
+x
+
=
成立的实数x的取值集合为( )
| OA |
| OB |
| BC |
| 0 |
| A、{-1} | B、∅ |
| C、{0} | D、{0,-1} |
“sinA=
”是“A=45°”的( )
| ||
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
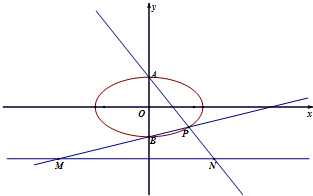 已知椭圆C:
已知椭圆C: