题目内容
已知矩阵
的一个特征值为4,求另一个特征值及其对应的一个特征向量.
|
|
考点:特征值与特征向量的计算
专题:选作题,矩阵和变换
分析:根据特征多项式的一个零点为4,可得x=2,再回代到方程f(λ)=0即可解出另一个特征值为λ2=-1.最后利用求特征向量的一般步骤,可求出其对应的一个特征向量.
解答:
解:矩阵的特征多项式为f(λ)=
=(λ-1)(λ-x)-6.
∵λ1=方4程f(λ)=0的一根,
∴(4-1)(4-x)-6=0,可得x=2.
∴方程f(λ)=0即(λ-1)(λ-2)-6=0,可得另一个特征值为:λ2=-1,
设λ2=-1对应的一个特征向量为
=
,
则
得x=-y,可令x=1,则y=-1,
∴矩阵的另一个特征值为-1,对应的一个特征向量为
=
.
|
∵λ1=方4程f(λ)=0的一根,
∴(4-1)(4-x)-6=0,可得x=2.
∴方程f(λ)=0即(λ-1)(λ-2)-6=0,可得另一个特征值为:λ2=-1,
设λ2=-1对应的一个特征向量为
| α |
|
则
|
∴矩阵的另一个特征值为-1,对应的一个特征向量为
| α |
|
点评:本题给出含有字母参数的矩阵,在知其一个特征值的情况下求另一个特征值和相应的特征向量,考查了特征值与特征向量的计算的知识,属于基础题.

练习册系列答案
相关题目
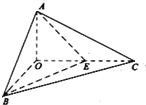 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.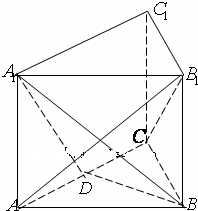 如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为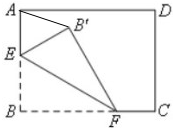 如图,在矩形ABCD中,AB=3,BC=4,点E、F分别在AB、BC边上,将△BEF沿EF折叠,点B落在B′处,当B′在矩形ABCD内部时,AB′的最小值为
如图,在矩形ABCD中,AB=3,BC=4,点E、F分别在AB、BC边上,将△BEF沿EF折叠,点B落在B′处,当B′在矩形ABCD内部时,AB′的最小值为