题目内容
在随机抽查某中学高二级140名学生是否晕机的情况中,已知男学生56人,其中晕机有28人;女学生中不会晕机的为56人.不会晕机的男学生中有2人成绩优秀,不会晕机的女生中有4人成绩优秀.
(1)完成下面2×2列联表的空白处;
(2)能否在犯错误的概率不超过0.05的前提下认为是否晕机与性别有关系?(k保留三位小数)
(3)若从不会晕机的6名成绩优秀的学生中随机抽取2人去国外参加数学竞赛,试求所抽取的2人中恰有一人是男学生、一人是女学生的概率.(4分)
注:①参考公式:K2=
,其中n=a+b+c+d.
②常用数据表如下:
(1)完成下面2×2列联表的空白处;
| 晕机 | 不会晕机 | 合计 | |
| 男学生 | 28 | 56 | |
| 女学生 | 56 | ||
| 合计 | 140 |
(3)若从不会晕机的6名成绩优秀的学生中随机抽取2人去国外参加数学竞赛,试求所抽取的2人中恰有一人是男学生、一人是女学生的概率.(4分)
注:①参考公式:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
②常用数据表如下:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
考点:独立性检验的应用
专题:综合题,概率与统计
分析:(1)根据条件中所给的数据,写出列联表,注意各个部分的数据不要写错位置,做出合计要填在表中.
(2)根据列联表和求观测值的公式,把数据代入公式,求出观测值,把观测值同临界值进行比较,得到在犯错误的概率不超过0.05的前提下我们认为是“晕机与性别”有关.
(3)利用列举法确定基本事件的个数,即可求出所抽取的2人中恰有一人是男学生、一人是女学生的概率.
(2)根据列联表和求观测值的公式,把数据代入公式,求出观测值,把观测值同临界值进行比较,得到在犯错误的概率不超过0.05的前提下我们认为是“晕机与性别”有关.
(3)利用列举法确定基本事件的个数,即可求出所抽取的2人中恰有一人是男学生、一人是女学生的概率.
解答:
解:(1)2×2列联表如下:
(2)根据列联表中的数据,得到K2的观测值为:k=
=
≈3.889>3.841…(8分)
因此,在犯错误的概率不超过0.05的前提下,认为是否晕机与性别有关系.…(10分)
(3)设不会晕机的2名成绩优秀的男学生的编号为A,B,不会晕机的4名成绩优秀的女学生的编号是C,D,E,F,则从不会晕机的6名成绩优秀的学生中,随机抽取2人的基本事件有:AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,共15个,
其中恰有一人是男学生,一人是女学生的基本事件有:
AC,AD,AE,AF,BC,BD,BE,BF,共8个.…(12分)
所以,所抽取的2人中恰有一人是男学生,一人是女学生的概率是
…(14分)
| 晕机 | 不会晕机 | 合计 | |
| 男乘客 | 28 | 28 | 56 |
| 女乘客 | 28 | 56 | 84 |
| 合计 | 56 | 84 | 140 |
| 140×(28×56-28×28)2 |
| 56×84×56×84 |
| 35 |
| 9 |
因此,在犯错误的概率不超过0.05的前提下,认为是否晕机与性别有关系.…(10分)
(3)设不会晕机的2名成绩优秀的男学生的编号为A,B,不会晕机的4名成绩优秀的女学生的编号是C,D,E,F,则从不会晕机的6名成绩优秀的学生中,随机抽取2人的基本事件有:AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,共15个,
其中恰有一人是男学生,一人是女学生的基本事件有:
AC,AD,AE,AF,BC,BD,BE,BF,共8个.…(12分)
所以,所抽取的2人中恰有一人是男学生,一人是女学生的概率是
| 8 |
| 15 |
点评:本题考查古典概型概率的计算,考查独立性检验的应用,这种问题解题时关键要看清题意,看出各种情况下的量,注意在数字运算上不要出错.

练习册系列答案
相关题目
已知椭圆O:
+
=1的离心率为e1,动△ABC是其内接三角形,且
=
+
.若AB的中点为D,D的轨迹E的离心率为e2,则( )
| x2 |
| a2 |
| y2 |
| b2 |
| OC |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
| A、e1=e2 |
| B、e1<e2 |
| C、e1>e2 |
| D、e1e2=1 |
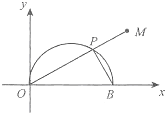 在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度.
在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度. 如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,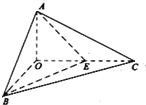 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.