题目内容
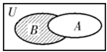已知全集U={x∈N|0＜x≤8}，集合A={1，2，4，5}，B={3，5，7，8}，则图中阴影部分所表示的集合是（ ）| A、{1，2，4} |
| B、{3，7，8} |
| C、{1，2，4，6} |
| D、{3，6，7，8} |
考点：Venn图表达集合的关系及运算
专题：集合
分析：由阴影部分可再对应的集合为∁UA∩B，即可得到结论．
解答：
解：由图象可知阴影部分可再对应的集合为∁UA∩B，
∵全集U={x∈N|0＜x≤8}，集合A={1，2，4，5}，B={3，5，7，8}，
∴（∁UA）∩B={3，7，8}，
故选：B．
∵全集U={x∈N|0＜x≤8}，集合A={1，2，4，5}，B={3，5，7，8}，
∴（∁UA）∩B={3，7，8}，
故选：B．
点评：本题主要考查集合的基本运算，比较基础．
练习册系列答案
相关题目
不等式（x-5）（6-x）＞6-x的解集是（ ）
| A、（5，+∞） |
| B、（6，+∞） |
| C、∅ |
| D、（-∞，5），（6，+∞） |
平面内有n个圆，其中每两个圆都相交于两点，且每三个圆都不共点，用f（n）表示这n个圆把平面分割的区域数，那么f（n+1）与f（n）之间的关系为（ ）
| A、f（n+1）=f（n）+n |
| B、f（n+1）=f（n）+2n |
| C、f（n+1）=f（n）+n+1 |
| D、f（n+1）=f（n）+n-1 |
已知A、B、C是直线l上不同的三个点，点O不在直线l上，则使等式x2
+x
+
=
成立的实数x的取值集合为（ ）
| OA |
| OB |
| BC |
| 0 |
| A、{-1} | B、∅ |
| C、{0} | D、{0，-1} |
已知椭圆O：
+
=1的离心率为e1，动△ABC是其内接三角形，且
=
+
．若AB的中点为D，D的轨迹E的离心率为e2，则（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| OC |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
| A、e1=e2 |
| B、e1＜e2 |
| C、e1＞e2 |
| D、e1e2=1 |
在空间直坐标系中，点P在x轴上，它到P1（0，
，3）的距离为2
，则点P的坐标为（ ）
| 2 |
| 3 |
| A、（0，1，0）或（0，-1，0） |
| B、（1，0，0） |
| C、（1，0，0）或（-1，0，0） |
| D、（0，1，0）或（0，0，1） |
“sinA=
”是“A=45°”的（ ）
| ||
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |