题目内容
已知p:直线x-2y+3=0与抛物线y2=ax(a>0)没有交点;q:方程
+
=1表示椭圆;若p∧q为真命题,试求实数a的取值范围.
| x2 |
| 4-a |
| y2 |
| a-1 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由p∧q为真命题,得p为真命题且q为真命题;p为真命题时求出a的取值范围,q为真命题时求出a的取值范围,取交集即可.
解答:
解:∵p∧q为真命题,∴p为真命题且q为真命题;
命题p:
,
消去x,得y2-2ay+3a=0;
∵直线与抛物线没有交点,
∴△=4a2-12a<0,解得0<a<3;
命题q:方程
+
=1表示椭圆,
则
;
解得1<a<4,且a≠
;
由上可知,a的取值范围是(1,
)∪(
,3).
命题p:
|
消去x,得y2-2ay+3a=0;
∵直线与抛物线没有交点,
∴△=4a2-12a<0,解得0<a<3;
命题q:方程
| x2 |
| 4-a |
| y2 |
| a-1 |
则
|
解得1<a<4,且a≠
| 5 |
| 2 |
由上可知,a的取值范围是(1,
| 5 |
| 2 |
| 5 |
| 2 |
点评:本题通过复合命题的真假,考查了圆锥曲线的应用问题,解题时应根据复合命题的真假性,求出命题成立的条件是什么,从而解出结果,是基础题.

练习册系列答案
相关题目
在空间直坐标系中,点P在x轴上,它到P1(0,
,3)的距离为2
,则点P的坐标为( )
| 2 |
| 3 |
| A、(0,1,0)或(0,-1,0) |
| B、(1,0,0) |
| C、(1,0,0)或(-1,0,0) |
| D、(0,1,0)或(0,0,1) |
 如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,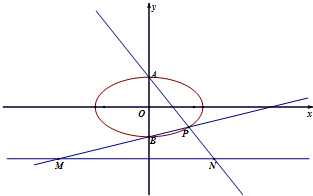 已知椭圆C:
已知椭圆C: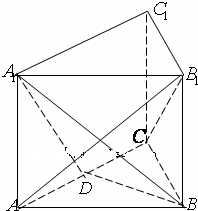 如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为