题目内容
已知函数f(x)=x-1-2lnx
(1)求曲线f(x)在点(1,f(x))处的切线方程;
(2)求f(x)的单调区间.
(1)求曲线f(x)在点(1,f(x))处的切线方程;
(2)求f(x)的单调区间.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)求出原函数的导函数,得到函数在x=1时的导数,再求得f(1),然后利用直线方程的点斜式得答案;
(2)求出导函数的零点,由导函数的零点对定义域分段,由导函数在不同区间段内的符号得到原函数的单调期间.
(2)求出导函数的零点,由导函数的零点对定义域分段,由导函数在不同区间段内的符号得到原函数的单调期间.
解答:
解:(1)由f(x)=x-1-2lnx,得f′(x)=1-
,则f′(1)=-1,
又f(1)=1-1-2ln1=0,
∴曲线f(x)在点(1,f(1))处的切线方程为y=-1×(x-1),
即x+y-1=0;
(2)由(1)知f′(x)=1-
(x>0),
当x∈(2,+∞)时,f′(x)>0,f(x)为增函数;
当x∈(0,2)时,f′(x)<0,f(x)为减函数.
| 2 |
| x |
又f(1)=1-1-2ln1=0,
∴曲线f(x)在点(1,f(1))处的切线方程为y=-1×(x-1),
即x+y-1=0;
(2)由(1)知f′(x)=1-
| 2 |
| x |
当x∈(2,+∞)时,f′(x)>0,f(x)为增函数;
当x∈(0,2)时,f′(x)<0,f(x)为减函数.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的单调区间,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若p是真命题,q是假命题,以下四个命题:p且q,p或q,非p,非q,其中假命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
函数f(x)=sin(x-
)的图象的一个对称中心是( )
| π |
| 4 |
| A、(-π,0) | ||
B、(-
| ||
C、(
| ||
D、(
|
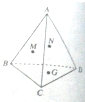 如图,已知A为平面BCD外一点,M,N,G分别是△ABC、△ABD、△BCD的重心,求证:平面MNG∥平面ACD.
如图,已知A为平面BCD外一点,M,N,G分别是△ABC、△ABD、△BCD的重心,求证:平面MNG∥平面ACD.