题目内容
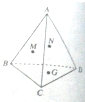如图，已知A为平面BCD外一点，M，N，G分别是△ABC、△ABD、△BCD的重心，求证：平面MNG∥平面ACD．考点：平面与平面平行的判定
专题：空间位置关系与距离
分析：连接AM，AN，并延长分别交BC，BD与D，E，由三角形重心的性质得到AM：AD=AN：AE=2：3，进一步得到MN∥CD，
同理MG∥CD，结合面面平行的判定定理可证．
同理MG∥CD，结合面面平行的判定定理可证．
解答：
证明：连接AM，AN，并延长分别交BC，BD与D，E，
因为M，N，G分别是△ABC、△ABD、△BCD的重心，
所以AM：AD=AN：AE=2：3，
所以MN∥DE，又DE∥CD，
所以MN∥CD，
又MN?平面ACD，CD?平面ACD，
所以MN∥平面ACD．
同理MG∥AD，得到MG∥平面ACD，
又MN∩MG=M，
所以平面MNG∥平面ACD．
因为M，N，G分别是△ABC、△ABD、△BCD的重心，
所以AM：AD=AN：AE=2：3，
所以MN∥DE，又DE∥CD，
所以MN∥CD，
又MN?平面ACD，CD?平面ACD，
所以MN∥平面ACD．
同理MG∥AD，得到MG∥平面ACD，
又MN∩MG=M，
所以平面MNG∥平面ACD．
点评：本题考查了面面平行的判定定理的运用；一般的，要证面面平行只要证线面平行，进一步只要证线线平行，体现了转化的思想．
练习册系列答案
相关题目
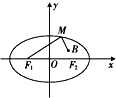如图，已知椭圆
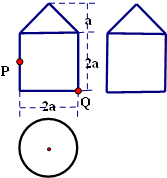一个几何体的三视图及部分度量值如图所示，其中，正视图与侧视图都是由一个正方形和一个等腰三角形组成，俯视图是一个圆．