题目内容

若实数x，y满足|x+1|+（y-1）2=0，则x+y=
 
．
考点：曲线与方程
专题：函数的性质及应用
分析：利用非负数，求出x，y的值，即可求解x+y的值．
解答： 解：实数x，y满足|x+1|+（y-1）2=0，
可得x+1=0．解得x=-1，y-1=0，解得y=1
所以x+y=-1+1=0．
故答案为：0．
点评：本题考查函数与方程的应用，函数的零点，注意非负数的应用，考查计算能力．
练习册系列答案
相关题目
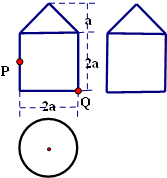一个几何体的三视图及部分度量值如图所示，其中，正视图与侧视图都是由一个正方形和一个等腰三角形组成，俯视图是一个圆．
（1）判断该几何体的结构特征，并求其表面积；
（2）如果正视图中的点P是其所在线段的中点，点Q是其所在正方形的顶点，试求：在原几何体的侧面上，从P点到Q点的最短路径的长．
已知二次函数f（x）=2x2+ax+b为偶函数，g（x）=（
3
-1）x+m，h（x）=c（x+1）2（c≠2），关于x的方程f（x）=h（x）有且仅有一根
1
2
．
（Ⅰ）求a，b，c的值；
（Ⅱ）若对任意的x∈[-1，1]，
f(x)
≤g（|x|）恒成立，求实数m的取值范围；
（Ⅲ）令φ（x）=
f(x)
+
f(1-x)
，若存在x1，x2∈[0，1]使得|φ（x1）-φ（x2）|≥g（m），求实数m的取值范围．
已知命题p：x2+2x-3＞0；命题q：
3-x
＜1，若“非q且p”为真，则x的取值范围是
 
．
已知函数f（x）=x-1-2lnx
（1）求曲线f（x）在点（1，f（x））处的切线方程；
（2）求f（x）的单调区间．
关于x的一元二次方程x2-5x+a2=0的一个根是0，则a的值是（　　）
A、0B、1C、-1D、0，或-1
已知不等式组
x2-x-2＞0
2x2+(5+2k)x+5k＜0.

（1）当k=0时，求不等式组的解区间；
（2）若不等式组的整数解只有一个-2，求实数k的取值范围．
已知函数f（x）=ax2+bx+c（a≠0）的图象过点A（0，1）和B（-1，0），且b2-4a≤0．求f（x）的解析式．
a、b为实数，集合M={
b
a
，1}，N={a，0}，f：x→2x表示把集合M中的元素x，映射到集合N中为2x，则a+b等于（　　）
A、-2B、0C、2D、±2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网