题目内容
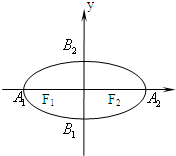 如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )
如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )A、(
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据题意得出∠B1PA2是向量
与
的夹角,设出椭圆的方程,利用坐标表示出
、
;再由数量积
•
<0,求出椭圆离心率的取值范围.
| B2A2 |
| F2B1 |
| B2A2 |
| F2B1 |
| B2A2 |
| F2B1 |
解答:
解: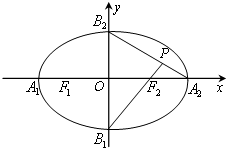 如图所示,
如图所示,
∠B1PA2是
与
的夹角;
设椭圆的长半轴、短半轴、半焦距分别为a,b,c,
则
=(a,-b),
=(-c,-b);
∵向量的夹角为钝角时,
•
<0,
∴-ac+b2<0,
又b2=a2-c2,
∴a2-ac-c2<0;
两边除以a2得1-e-e2<0,
即e2+e-1>0;
解得e<
,或e>
;
又∵0<e<1,∴
<e<1;
∴椭圆离心率e的取值范围是(
,1).
故选:D.
 如图所示,
如图所示,∠B1PA2是
| B2A2 |
| F2B1 |
设椭圆的长半轴、短半轴、半焦距分别为a,b,c,
则
| B2A2 |
| F2B1 |
∵向量的夹角为钝角时,
| B2A2 |
| F2B1 |
∴-ac+b2<0,
又b2=a2-c2,
∴a2-ac-c2<0;
两边除以a2得1-e-e2<0,
即e2+e-1>0;
解得e<
-1-
| ||
| 2 |
-1+
| ||
| 2 |
又∵0<e<1,∴
-1+
| ||
| 2 |
∴椭圆离心率e的取值范围是(
-1+
| ||
| 2 |
故选:D.
点评:本题考查了椭圆的几何性质的应用问题,解题时利用向量的数量积小于0,建立不等式,求出正确的结论,是中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
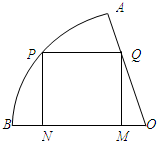 如图,在半径为
如图,在半径为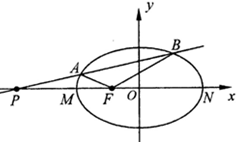 如图,点F是椭圆
如图,点F是椭圆