题目内容
设全集U=R，集合A={x|-1≤x≤3}，B={x|2x-4≥x-2}．
（1）求∁U（A∩B）；
（2）若集合C={x|2x+a＞0}，满足B⊆C，求实数a的取值范围．
（1）求∁U（A∩B）；
（2）若集合C={x|2x+a＞0}，满足B⊆C，求实数a的取值范围．
考点：交、并、补集的混合运算
专题：集合
分析：（1）根据集合的基本运算，即可求出∁U（A∩B）；
（2）根据集合之间的关系，即可得到结论．
（2）根据集合之间的关系，即可得到结论．
解答：
解：（1）∵B={x|2x-4≥x-2}={x|x≥2}，A={x|-1≤x≤3}，
∴A∩B={x|2≤x≤3}，则∁U（A∩B）={x|x＞3或x＜2}．
（2）C={x|2x+a＞0}{x|x＞-
}，
若B⊆C，
则-
＜2，解得a＞-4，
故实数a的取值范围是（-4，+∞）
∴A∩B={x|2≤x≤3}，则∁U（A∩B）={x|x＞3或x＜2}．
（2）C={x|2x+a＞0}{x|x＞-
| a |
| 2 |
若B⊆C，
则-
| a |
| 2 |
故实数a的取值范围是（-4，+∞）
点评：本题主要考查集合的基本运算以及集合关系的应用．难度不大．
练习册系列答案
阅读快车系列答案
相关题目
在五面体ABCDEF中，已知DE⊥平面ABCD，AD∥BC，求证：BC∥EF．若角α的终边在直线y=-2x上，且sinα＞0，则cosα和tana的值分别为（ ）
A、
| ||||||
B、-
| ||||||
C、-
| ||||||
D、-
|
已知集合A={x|-10≤x≤10}，B={x|x≤15}，则A∪B=（ ）
| A、{x|-10≤x≤15} |
| B、{x|-10≤x＜10} |
| C、{x|x≤15} |
| D、{x|x＜10} |
椭圆的中心为O，左焦点为F1，P是椭圆上的一点，已知△PF1O为正三角形，则P到右准线的距离与长半轴的长之比是（ ）
A、
| ||
B、3-
| ||
C、
| ||
| D、1 |
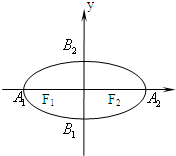如图，椭圆的中心在坐标原点，焦点在x轴上，A1，A2，B1，B2椭圆顶点，F2为右焦点，延长B1F2与A2B2交于点P，若∠B1PA2为钝角，则该椭圆离心率的取值范围是（ ）A、（
| ||||
B、（0，
| ||||
C、（0，
| ||||
D、（
|
定义在R上的函数f（x）满足下列三个条件：（1）f（x+3）=-
；（2）对任意3≤x1＜x2≤6，都有f（x1）＜f（x2）；（3）y=f（x+3）的图象关于y轴对称．则下列结论中正确的是（ ）
| 1 |
| f(x) |
| A、f（3）＜f（7）＜f（4.5） |
| B、f（3）＜f（4.5）＜f（7） |
| C、f（7）＜f（4.5）＜f（3） |
| D、f（7）＜f（3）＜f（4.5） |