题目内容
数列{an}中满足a1=a,an+1=
.
(1)求出a2,a3,a4.
(2)猜想通项公式an
(3)用数学归纳法证明通项公式.
| 1 |
| 2-an |
(1)求出a2,a3,a4.
(2)猜想通项公式an
(3)用数学归纳法证明通项公式.
考点:数学归纳法
专题:综合题,点列、递归数列与数学归纳法
分析:(1)根据数列{an}中满足a1=a,an+1=
,求出a2,a3,a4.
(2)总结出规律求出an;
(3)利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
| 1 |
| 2-an |
(2)总结出规律求出an;
(3)利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答:
解:(1)∵a1=a,an+1=
,
∴a2=
,a3=
,a4=
;
(2)由(1)猜想通项公式an=
;
(3)①n=1时,成立,
②假设n=k时成立,即ak=
,
则n=k+1时,ak+1=
=
=
,
即n=k+1时,成立.
由①②可知an=
.
| 1 |
| 2-an |
∴a2=
| 1 |
| 2-a |
| 2-a |
| 3-2a |
| 3-2a |
| 4-3a |
(2)由(1)猜想通项公式an=
| (n-1)-(n-2)a |
| n-(n-1)a |
(3)①n=1时,成立,
②假设n=k时成立,即ak=
| (k-1)-(k-2)a |
| k-(k-1)a |
则n=k+1时,ak+1=
| 1 |
| 2-ak |
| 1 | ||
2-
|
| k-(k-1)a |
| k+1-ka |
即n=k+1时,成立.
由①②可知an=
| (n-1)-(n-2)a |
| n-(n-1)a |
点评:此题主要考查归纳法的证明,归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而求证,这是数列的通项一种常用求解的方法.

练习册系列答案
相关题目
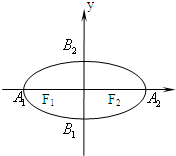 如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )
如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )A、(
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
定义在R上的函数f(x)满足下列三个条件:(1)f(x+3)=-
;(2)对任意3≤x1<x2≤6,都有f(x1)<f(x2);(3)y=f(x+3)的图象关于y轴对称.则下列结论中正确的是( )
| 1 |
| f(x) |
| A、f(3)<f(7)<f(4.5) |
| B、f(3)<f(4.5)<f(7) |
| C、f(7)<f(4.5)<f(3) |
| D、f(7)<f(3)<f(4.5) |
五件产品中有两件次品三件正品,从中任取两件检验恰好都是正品的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
程序:输入2,3,则程序执行的结果为( )


| A、2,3 | B、3,2 |
| C、2,2 | D、3,3 |
已知x>4,则f(x)=
有( )
| x2-4x+1 |
| x-4 |
| A、最大值-6 | B、最小值6 |
| C、最大值-2 | D、最小值2 |
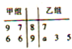 如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=