题目内容
若2a＞1，则a的取值范围为 ．
考点：指数函数的图像与性质
专题：计算题,函数的性质及应用
分析：2a＞1=20，且y=2x在R上是增函数，从而求解．
解答：
解：∵2a＞1=20，
又∵y=2x在R上是增函数，
∴a＞0．
故答案为：a＞0．
又∵y=2x在R上是增函数，
∴a＞0．
故答案为：a＞0．
点评：本题考查了指数函数的单调性的判断与应用，属于基础题．
练习册系列答案
相关题目
若角α的终边在直线y=-2x上，且sinα＞0，则cosα和tana的值分别为（ ）
A、
| ||||||
B、-
| ||||||
C、-
| ||||||
D、-
|
椭圆的中心为O，左焦点为F1，P是椭圆上的一点，已知△PF1O为正三角形，则P到右准线的距离与长半轴的长之比是（ ）
A、
| ||
B、3-
| ||
C、
| ||
| D、1 |
某公司为了公司周年庆典，先将公司门前广场进行装饰，广场上有一垂直于地面的墙面AB高8+8
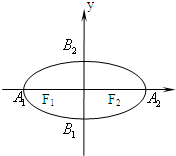如图，椭圆的中心在坐标原点，焦点在x轴上，A1，A2，B1，B2椭圆顶点，F2为右焦点，延长B1F2与A2B2交于点P，若∠B1PA2为钝角，则该椭圆离心率的取值范围是（ ）A、（
| ||||
B、（0，
| ||||
C、（0，
| ||||
D、（
|
已知奇函数f（x）在x≥0时的图象如图所示，则不等式f（x）＜0的解集为（ ）
| A、（-1，0）∪（1，2） |
| B、（-∞，2）∪（-1，0）∪（1，2） |
| C、（-2，-1）∪（1，2） |
| D、（-1，0）∪（0，1） |
程序：输入2，3，则程序执行的结果为（ ）
| A、2，3 | B、3，2 |
| C、2，2 | D、3，3 |