题目内容
已知函数f(x)=kex-2,g(x)=
,若k>0,对于?x>0,均有f(x)≥g(x)成立,求正实数k的范围.
| 2kx-k-1 |
| x |
考点:函数恒成立问题
专题:导数的综合应用
分析:由于k>0,对?x>0,均有f(x)≥g(x)成立,可得k>0,对?x>0,f(x)-g(x)=kex+
-2k-2≥0恒成立?u(x)=kxex-(2k+2)x+(k+1)≥0,k>0,?x>0.利用研究函数的单调性极值即可得出.
| k+1 |
| x |
解答:
解:∵k>0,对?x>0,均有f(x)≥g(x)成立,
∴k>0,对?x>0,f(x)-g(x)=kex+
-2k-2≥0恒成立
?u(x)=kxex-(2k+2)x+(k+1)≥0,k>0,?x>0.
u′(x)=kex+kxex-(2k+2)=v(x),
v′(x)=k(2+x)ex>0,
∴v(x)即u′(x)在(0,+∞)上单调递增,
而u′(0)=-k-2<0,x→+∞,u′(x)>0.
∴u(x)存在极小值点.
令u′(x0)=0,
kex0+kx0ex0-(2k+2)=0,
∴ex0=
,k=
.
则u(x0)=kx0ex0-(2k+2)x0+(k+1)=
≥0,
∴2 x02-x0-1≤0,
解得0<x0≤1.
∴0<ex0+x0ex0≤2e-2,
则k≥
.
∴k的取值范围是[
,+∞).
∴k>0,对?x>0,f(x)-g(x)=kex+
| k+1 |
| x |
?u(x)=kxex-(2k+2)x+(k+1)≥0,k>0,?x>0.
u′(x)=kex+kxex-(2k+2)=v(x),
v′(x)=k(2+x)ex>0,
∴v(x)即u′(x)在(0,+∞)上单调递增,
而u′(0)=-k-2<0,x→+∞,u′(x)>0.
∴u(x)存在极小值点.
令u′(x0)=0,
kex0+kx0ex0-(2k+2)=0,
∴ex0=
| 2k+2 |
| k+kx0 |
| 2 |
| ex0+x0ex0-2 |
则u(x0)=kx0ex0-(2k+2)x0+(k+1)=
| (2k+2)x0-(2k+2)x0(1+x0)+(k+1)(1+x0) |
| 1+x0 |
∴2 x02-x0-1≤0,
解得0<x0≤1.
∴0<ex0+x0ex0≤2e-2,
则k≥
| 1 |
| e-1 |
∴k的取值范围是[
| 1 |
| e-1 |
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了多次求导解决问题,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
李先生有10000美元,准备用于储蓄,结果他储蓄时人民币一年定期存款利率是3%,美元是4%,汇率是1美元=6.9元人民币,一年后人民币一年定期存款利率调整为4%,美元调整为3%,汇率是1美元=6.8元人民币,李先生一年定期储蓄可能获得的最大本息收益为(注:定期储蓄存款在存期内遇有利率调整,按存单开户日的定期储蓄存款利率计付利息)( )
| A、72720元 |
| B、10400美元 |
| C、74880元 |
| D、10451美元 |
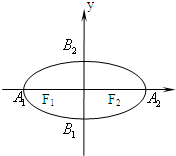 如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )
如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )A、(
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
 在五面体ABCDEF中,已知DE⊥平面ABCD,AD∥BC,求证:BC∥EF.
在五面体ABCDEF中,已知DE⊥平面ABCD,AD∥BC,求证:BC∥EF.