题目内容
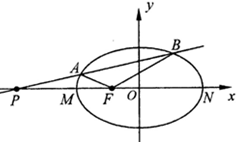 如图,点F是椭圆
如图,点F是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆的标准方程;
(2)过点P的直线与椭圆相交于两点A、B,求证:∠AFM=∠BFN;
(3)记△ABF的面积为S,求S的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得
,由此能求出椭圆方程.
(2)当直线AB的斜率为0时,成立;当直线AB的斜率不为0时,设AB的方程为x=my-8,代入椭圆方程整理,得:(3m2+4)y2-48my+144=0,由此利用韦达定理结合已知条件能证明∠AFM=∠BFN.
(3)由已知条件推导出S=S△PBF-S△PAF≤3
,由此能求出△ABF的面积S的最大值为3
.
|
(2)当直线AB的斜率为0时,成立;当直线AB的斜率不为0时,设AB的方程为x=my-8,代入椭圆方程整理,得:(3m2+4)y2-48my+144=0,由此利用韦达定理结合已知条件能证明∠AFM=∠BFN.
(3)由已知条件推导出S=S△PBF-S△PAF≤3
| 3 |
| 3 |
解答:
(1)解:∵|MN|=8,且该椭圆的离心率为
,
∴
,
解得a=4,b=
,
∴椭圆方程为
+
=1.
(2)证明:当直线AB的斜率为0时,∠AFM=∠BFM=0°,成立;
当直线AB的斜率不为0时,设AB的方程为x=my-8,
代入椭圆方程整理,得:(3m2+4)y2-48my+144=0,
∴△=576(m2-4),设A(xA,yA),B(xB,yB),
yA+yB=
,yAyB=
,
∴kAF+kBF=
+
=
+
=
=
,
∵2myAyB-6(yA+yB)=2m•
-6•
=0,
∴kAF=-kBF,
∴∠AFM=∠BFN.
(3)解:S=S△PBF-S△PAF=
•|PF|•|yB-yA|
=
=
=
≤
=3
,
当且仅当3
=
,即m=±
(此时△>0)时取等号,
∴△ABF的面积S的最大值为3
.
| 1 |
| 2 |
∴
|
解得a=4,b=
| 12 |
∴椭圆方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)证明:当直线AB的斜率为0时,∠AFM=∠BFM=0°,成立;
当直线AB的斜率不为0时,设AB的方程为x=my-8,
代入椭圆方程整理,得:(3m2+4)y2-48my+144=0,
∴△=576(m2-4),设A(xA,yA),B(xB,yB),
yA+yB=
| 48m |
| 3m2+4 |
| 144 |
| 3m2+4 |
∴kAF+kBF=
| yA |
| xA+2 |
| yB |
| xB+2 |
| yA |
| myA-6 |
| yB |
| myB-6 |
=
| yA(myB-6)(myA-6) |
| (myA-6)(myB-6) |
=
| 2myAyB-6(yA+yB) |
| (myA-6)(myB-6) |
∵2myAyB-6(yA+yB)=2m•
| 144 |
| 3m2+4 |
| 48m |
| 3m2+4 |
∴kAF=-kBF,
∴∠AFM=∠BFN.
(3)解:S=S△PBF-S△PAF=
| 1 |
| 2 |
=
72•
| ||
| 3m2+4 |
=
72
| ||
| 3(m2-4)+16 |
=
| 72 | ||||||
3
|
≤
| 72 | ||
2
|
| 3 |
当且仅当3
| m2-4 |
| 16 | ||
|
2
| ||
| 3 |
∴△ABF的面积S的最大值为3
| 3 |
点评:本题考查椭圆的标准方程的求法,考查两角相等的证明,考查三角形面积的最大值的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
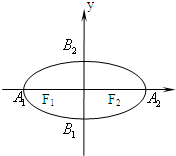 如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )
如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )A、(
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
已知奇函数f(x)在x≥0时的图象如图所示,则不等式f(x)<0的解集为( )


| A、(-1,0)∪(1,2) |
| B、(-∞,2)∪(-1,0)∪(1,2) |
| C、(-2,-1)∪(1,2) |
| D、(-1,0)∪(0,1) |
定义在R上的函数f(x)满足下列三个条件:(1)f(x+3)=-
;(2)对任意3≤x1<x2≤6,都有f(x1)<f(x2);(3)y=f(x+3)的图象关于y轴对称.则下列结论中正确的是( )
| 1 |
| f(x) |
| A、f(3)<f(7)<f(4.5) |
| B、f(3)<f(4.5)<f(7) |
| C、f(7)<f(4.5)<f(3) |
| D、f(7)<f(3)<f(4.5) |
五件产品中有两件次品三件正品,从中任取两件检验恰好都是正品的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
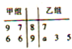 如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=