题目内容
已知函数f(x)=2sinx(sinx+cosx).
(1)求f(x)的最小正周期;
(2)求出函数y=f(x)在区间[-
,
]上的单调递减区间.
(1)求f(x)的最小正周期;
(2)求出函数y=f(x)在区间[-
| π |
| 2 |
| π |
| 2 |
考点:二倍角的余弦,复合三角函数的单调性
专题:三角函数的求值
分析:(1)f(x)解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式即可求出最小正周期;
(2)由x的范围确定出2x-
的范围,利用正弦函数的单调性求出f(x)在区间[-
,
]上的单调递减区间即可.
(2)由x的范围确定出2x-
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
解答:
解 (1)f(x)=2sin2x+2sinxcosx=2×
+sin2x=1+sin2x-cos2x=1+
sin(2x-
),
∵ω=2,∴T=
=π,
则f(x)的最小正周期为π;
(2)∵x∈[-
,
],
∴2x-
∈[-
,
],
令-
≤2x-
≤-
或
≤2x-
≤
,
解得:-
≤x≤-
或
≤x≤
,
则函数y=f(x)在区间[-
,
]上的单调递减区间为[-
,-
]∪[
,
].
| 1-cos2x |
| 2 |
| 2 |
| π |
| 4 |
∵ω=2,∴T=
| 2π |
| 2 |
则f(x)的最小正周期为π;
(2)∵x∈[-
| π |
| 2 |
| π |
| 2 |
∴2x-
| π |
| 4 |
| 5π |
| 4 |
| 3π |
| 4 |
令-
| 5π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
解得:-
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 2 |
则函数y=f(x)在区间[-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 2 |
点评:此题考查了二倍角的正弦函数公式,两角和与差的正弦函数公式,以及正弦函数的单调性,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
椭圆的中心为O,左焦点为F1,P是椭圆上的一点,已知△PF1O为正三角形,则P到右准线的距离与长半轴的长之比是( )
A、
| ||
B、3-
| ||
C、
| ||
| D、1 |
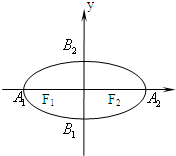 如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )
如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )A、(
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
已知奇函数f(x)在x≥0时的图象如图所示,则不等式f(x)<0的解集为( )


| A、(-1,0)∪(1,2) |
| B、(-∞,2)∪(-1,0)∪(1,2) |
| C、(-2,-1)∪(1,2) |
| D、(-1,0)∪(0,1) |
定义在R上的函数f(x)满足下列三个条件:(1)f(x+3)=-
;(2)对任意3≤x1<x2≤6,都有f(x1)<f(x2);(3)y=f(x+3)的图象关于y轴对称.则下列结论中正确的是( )
| 1 |
| f(x) |
| A、f(3)<f(7)<f(4.5) |
| B、f(3)<f(4.5)<f(7) |
| C、f(7)<f(4.5)<f(3) |
| D、f(7)<f(3)<f(4.5) |