题目内容
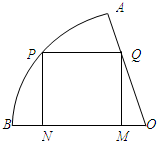 如图,在半径为
如图,在半径为| 3 |
(Ⅰ)将y表示成θ的函数关系式,并写出定义域;
(Ⅱ)在△ABC中,角A,B,C所对的边分别是a,b,c,若y取最大值时A=θ+
| π |
| 12 |
| 10 |
2
| ||
| 5 |
考点:函数模型的选择与应用
专题:三角函数的图像与性质,解三角形
分析:(Ⅰ)在Rt△PON中,PN=OPsinθ=
sinθ,ON=
cosθ.在Rt△OQM中,OM=
=sinθ.可得MN=0N-0M=
cosθ-sinθ.可得矩形PNMQ的面积y=PN•NM=
sinθ(
cosθ-sinθ),再利用倍角公式、两角和差的正弦公式即可得出.
(Ⅱ)当2θ+
=
时,y取得最大值,θ=
.可得A=
.由cosB=
,可得sinB=
.由正弦定理可得:b=
.利用两角和差的正弦公式可得sinC=sin(A+B)=sinAcosB+cosAsinB.由正弦定理可得:c=
.在△ABD中,由余弦定理可得:BD2=AB2+AD2-2AB•ADcosA.
| 3 |
| 3 |
| QM |
| tan60° |
| 3 |
| 3 |
| 3 |
(Ⅱ)当2θ+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 4 |
2
| ||
| 5 |
| 1-cos2B |
| asinB |
| sinA |
| asinC |
| sinA |
解答:
解:(Ⅰ)在Rt△PON中,PN=OPsinθ=
sinθ,ON=
cosθ.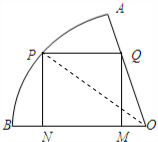
在Rt△OQM中,OM=
=
=sinθ.
∴MN=0N-0M=
cosθ-sinθ.
∴矩形PNMQ的面积y=PN•NM=
sinθ(
cosθ-sinθ)=3sinθcosθ-
sin2θ
=
sin2θ-
=
sin(2θ+
)-
,θ∈(0,
).
(Ⅱ)当2θ+
=
时,y取得最大值,θ=
.
∴A=
+
=
.
∵cosB=
,∴sinB=
=
.
由正弦定理可得:
=
,
∴b=
=
=2.
sinC=sin(A+B)=sinAcosB+cosAsinB=
×
+
×
=
.
由正弦定理可得:
=
,
∴c=
=
=3
.
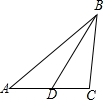
在△ABD中,由余弦定理可得:BD2=AB2+AD2-2AB•ADcosA
=(3
)2+12-2×3
×1×cos
=13.
∴BD=
.
D为AC中点,求BD的值.
| 3 |
| 3 |

在Rt△OQM中,OM=
| QM |
| tan60° |
| PN | ||
|
∴MN=0N-0M=
| 3 |
∴矩形PNMQ的面积y=PN•NM=
| 3 |
| 3 |
| 3 |
=
| 3 |
| 2 |
| ||
| 2 |
=
| 3 |
| π |
| 6 |
| ||
| 2 |
| π |
| 3 |
(Ⅱ)当2θ+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |

∴A=
| π |
| 6 |
| π |
| 12 |
| π |
| 4 |
∵cosB=
2
| ||
| 5 |
| 1-cos2B |
| ||
| 5 |
由正弦定理可得:
| a |
| sinA |
| b |
| sinB |
∴b=
| asinB |
| sinA |
| ||||||
|
sinC=sin(A+B)=sinAcosB+cosAsinB=
| ||
| 2 |
2
| ||
| 5 |
| ||
| 2 |
| ||
| 5 |
3
| ||
| 10 |
由正弦定理可得:
| a |
| sinA |
| c |
| sinC |
∴c=
| asinC |
| sinA |
| ||||||
|
| 2 |
在△ABD中,由余弦定理可得:BD2=AB2+AD2-2AB•ADcosA
=(3
| 2 |
| 2 |
| π |
| 4 |
∴BD=
| 13 |
D为AC中点,求BD的值.
点评:本题综合考查了直角三角形的边角关系、倍角公式、两角和差的正弦公式及其单调性、正弦定理余弦定理,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知集合A={x|-10≤x≤10},B={x|x≤15},则A∪B=( )
| A、{x|-10≤x≤15} |
| B、{x|-10≤x<10} |
| C、{x|x≤15} |
| D、{x|x<10} |
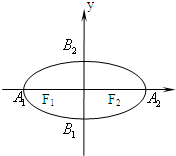 如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )
如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )A、(
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
