Question

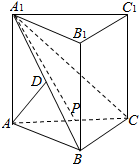如图，在直三棱柱ABC-A₁B₁C₁中，已知D点在直线A₁B上，AD⊥平面A₁BC．
（Ⅰ）求证：BC⊥AB；
（Ⅱ）若BC=2，AB=4，AD=2

3

，P为AC边的中点，求三棱锥P-A₁BC的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面垂直的性质

专题：空间位置关系与距离

分析：（Ⅰ）证明AD⊥BC，通过AA₁⊥平面ABC推出AA₁⊥BC，利用BC⊥平面A₁AB的性质定理证明BC⊥AB．
（Ⅱ）求出∠ABD=

π

3

，然后AA₁的值．利用V_P-A1BC=V_A1-PBC=

1

2

V_A1-ABC求解即可．

解答： （Ⅰ）证明：由AD⊥平面ABC，BC?平面ABC得AD⊥BC   ①
又AA₁⊥平面ABC⇒AA₁⊥BC   ②
AA₁∩AD=A     ③
由①②③得BC⊥平面A₁AB⇒BC⊥AB．

（Ⅱ）解：在Rt△ADB中，sin∠ABD=

2 3

4

=

3

2

，故∠ABD=

π

3

，
Rt△AA₁B中，AA₁=ABtan∠ABD=4

3

，
故V_P-A1BC=V_A1-PBC=

1

2

V_A1-ABC=

1

2

×

1

3

×

1

2

×2×4×4

3

=

8 3

3

即三棱锥P-A₁BC的体积为

8 3

3

．

点评：本题考查直线与平面平行的性质定理的应用，几何体的体积的求法，考查空间想象能力、计算能力以及推理能力．