题目内容
sin330°+(
-1)0+3 log32= .
| 2 |
考点:有理数指数幂的化简求值,运用诱导公式化简求值
专题:计算题,函数的性质及应用
分析:根据三角函数诱导公式,指数的0次幂以及对数的恒等式,进行计算即可.
解答:
解:原式=sin(360°-30°)+1+2
=sin(-30°)+3
=-sin30°+3
=-
+3
=
.
故答案为:
.
=sin(-30°)+3
=-sin30°+3
=-
| 1 |
| 2 |
=
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查了三角函数诱导公式,指数的0次幂以及对数的恒等式的应用问题,是基础题目.

练习册系列答案
相关题目
已知R是实数集,M={x|
<1},N={y|y=
},则(CRM)∩N=( )
| 2 |
| x |
| x-1 |
| A、(1,2) |
| B、[1,2] |
| C、[1,2) |
| D、[0,2] |
复数
(i为虚数单位)的虚部为( )
| 2+i |
| 2-i |
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合M={x|y2=3x,x∈R},N={y|x2+y2=4,x∈R,y∈R},则M∩N等于( )
| A、[-2,2] | ||||
| B、[-2,2] | ||||
C、{(1,
| ||||
| D、[0,2] |
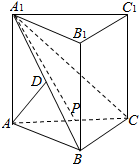 如图,在直三棱柱ABC-A1B1C1中,已知D点在直线A1B上,AD⊥平面A1BC.
如图,在直三棱柱ABC-A1B1C1中,已知D点在直线A1B上,AD⊥平面A1BC.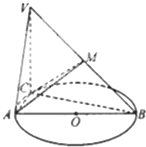 如图,已知⊙O的直径AB=3,点C为⊙O上异于A、B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.(Ⅰ)求证:BC⊥平面VAC
如图,已知⊙O的直径AB=3,点C为⊙O上异于A、B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.(Ⅰ)求证:BC⊥平面VAC