题目内容
已知等比数列{an}的公比q≠1,则下面说法中不正确的是( )
| A、{an+2+an}是等比数列 |
| B、对于k∈N*,k>1,ak-1+ak+1≠2ak |
| C、对于n∈N*,都有anan+2>0 |
| D、若a2>a1,则对于任意n∈N*,都有an+1>an |
考点:等比数列的性质
专题:综合题,等差数列与等比数列
分析:利用等比数列的通项,对选项分别进行分析,即可得出结论.
解答:
解:对于A,{an+2+an}是公比为q2的等比数列,正确;
对于B,对于k∈N*,k>1,ak-1+ak+1=
+akq,∵q≠1,∴ak-1+ak+1≠2ak,正确‘
对于C,anan+2=an2q2>0,正确;
对于D,若a2>a1,a>1,则对于任意n∈N*,都有an+1>an,故不正确,
故选:D.
对于B,对于k∈N*,k>1,ak-1+ak+1=
| ak |
| q |
对于C,anan+2=an2q2>0,正确;
对于D,若a2>a1,a>1,则对于任意n∈N*,都有an+1>an,故不正确,
故选:D.
点评:本题考查等比数列的通项,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
在二项式(x3-
)n(n∈N*)的展开式中,常数项为28,则n的值为( )
| 1 |
| x |
| A、12 | B、8 | C、6 | D、4 |
已知命题p:?x∈R,x-1>lnx.命题q:?x∈R,
>0,则( )
| x |
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∧(¬q)是真命题 |
| D、命题p∨(¬q)是假命题 |
已知R是实数集,M={x|
<1},N={y|y=
},则(CRM)∩N=( )
| 2 |
| x |
| x-1 |
| A、(1,2) |
| B、[1,2] |
| C、[1,2) |
| D、[0,2] |
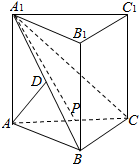 如图,在直三棱柱ABC-A1B1C1中,已知D点在直线A1B上,AD⊥平面A1BC.
如图,在直三棱柱ABC-A1B1C1中,已知D点在直线A1B上,AD⊥平面A1BC.