题目内容
已知函数f(x)=
sinωxsin(
+ωx)-cos2ωx-
(ω>0),其图象两相邻对称轴间的距离为
.
(Ⅰ)求ω的值;
(Ⅱ)设△ABC的内角A,B,C的对边分别为a,b,c,且c=
,f(C)=0,若向量
=(1,sinA)与向量
=(3,sinB)共线,求a,b的值.
| 3 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
(Ⅰ)求ω的值;
(Ⅱ)设△ABC的内角A,B,C的对边分别为a,b,c,且c=
| 7 |
| m |
| n |
考点:余弦定理,两角和与差的正弦函数
专题:三角函数的图像与性质,解三角形
分析:(Ⅰ)化简函数解析式可得f(x)=sin(2ωx-
)-1,由其图象两相邻对称轴间的距离为
,可得最小正周期为T=π,即可解得ω.
(Ⅱ)由(Ⅰ)可知sin(2C-
)=1,解得C=
,由已知
∥
可得b-3a=0①,由余弦定理,又已知c=
,即可解得7=a2+b2-ab②,联立方程可解得a,b的值.
| π |
| 6 |
| π |
| 2 |
(Ⅱ)由(Ⅰ)可知sin(2C-
| π |
| 6 |
| π |
| 3 |
| m |
| n |
| 7 |
解答:
解:(Ⅰ)f(x)=
sinωxsin(
+ωx)-cos2ωx-
=
sinωxcosωx-
-
=
sin2ωx-
cos2ωx-1
=sin(2ωx-
)-1
∵其图象两相邻对称轴间的距离为
.
∴最小正周期为T=π,
∴ω=1.
(Ⅱ)由(Ⅰ)可知:f(x)=sin(2x-
)-1
∴sin(2C-
)=1
∵0<C<π,
∴-
<2C-
<
,
∴2C-
=
,
即C=
由已知
∥
可得sinB-3sinA=0,
在△ABC中,由正弦定理可得b-3a=0①
由余弦定理可得:c2=a2+b2-2abcosC,
又已知c=
∴7=a2+b2-ab②
由①②联立,可解得:a=1,b=3.
| 3 |
| π |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 1+cos2ωx |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(2ωx-
| π |
| 6 |
∵其图象两相邻对称轴间的距离为
| π |
| 2 |
∴最小正周期为T=π,
∴ω=1.
(Ⅱ)由(Ⅰ)可知:f(x)=sin(2x-
| π |
| 6 |
∴sin(2C-
| π |
| 6 |
∵0<C<π,
∴-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
∴2C-
| π |
| 6 |
| π |
| 2 |
即C=
| π |
| 3 |
由已知
| m |
| n |
在△ABC中,由正弦定理可得b-3a=0①
由余弦定理可得:c2=a2+b2-2abcosC,
又已知c=
| 7 |
∴7=a2+b2-ab②
由①②联立,可解得:a=1,b=3.
点评:本题主要考查了两角和与差的正弦函数的应用,考查了余弦定理的应用,三角函数周期公式的应用,属于基本知识的考查.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
已知命题p:?x∈R,x-1>lnx.命题q:?x∈R,
>0,则( )
| x |
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∧(¬q)是真命题 |
| D、命题p∨(¬q)是假命题 |
在区间[-3,2]上随机选取一个数x,使得函数y=
有意义的概率为( )
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|

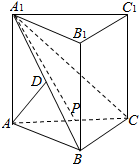 如图,在直三棱柱ABC-A1B1C1中,已知D点在直线A1B上,AD⊥平面A1BC.
如图,在直三棱柱ABC-A1B1C1中,已知D点在直线A1B上,AD⊥平面A1BC.