题目内容
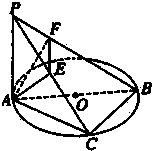 如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是
如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:利用线面垂直的判定与性质定理、圆的性质即可得出.
解答:
解:①∵AB是⊙O的直径,∴BC⊥AC,
∵PA⊥⊙O所在平面,∴PA⊥BC.
又PA∩AC=A,∴BC⊥平面PAC.
∵AE?平面PAC.
∴BC⊥AE.
因此①正确.
④由①可知:AE⊥BC,
又∵AE⊥PC,PC∩BC=C,
∴AE⊥平面PBC.
因此④正确.
②由④可知:AE⊥平面PBC,∴AE⊥PB.
又∵AF⊥PB,AE∩AF=A,
∴PB⊥平面AEF,
∴PB⊥EF.
因此②正确.
③AF⊥BC不正确;
用反证法证明:假设AF⊥BC,
又AF⊥PB,PB∩BC=B.
∴AF⊥平面PBC.
这与AE⊥平面PBC相矛盾.因此假设不成立.
故③不正确.
综上可知:只有①②④正确.
故答案为:①②④.
∵PA⊥⊙O所在平面,∴PA⊥BC.
又PA∩AC=A,∴BC⊥平面PAC.
∵AE?平面PAC.
∴BC⊥AE.
因此①正确.
④由①可知:AE⊥BC,
又∵AE⊥PC,PC∩BC=C,
∴AE⊥平面PBC.
因此④正确.
②由④可知:AE⊥平面PBC,∴AE⊥PB.
又∵AF⊥PB,AE∩AF=A,
∴PB⊥平面AEF,
∴PB⊥EF.
因此②正确.
③AF⊥BC不正确;
用反证法证明:假设AF⊥BC,
又AF⊥PB,PB∩BC=B.
∴AF⊥平面PBC.
这与AE⊥平面PBC相矛盾.因此假设不成立.
故③不正确.
综上可知:只有①②④正确.
故答案为:①②④.
点评:本题考查了线面垂直的判定与性质定理、圆的性质,属于中档题.

练习册系列答案
相关题目
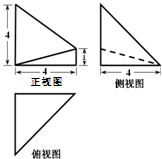 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )A、
| ||
B、
| ||
C、
| ||
| D、40 |
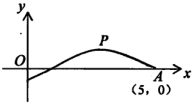 如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为
如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为