题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=
acosB.
(Ⅰ)求角B的大小;
(Ⅱ)若b=3,sinC=2sinA,求△ABC的面积.
| 3 |
(Ⅰ)求角B的大小;
(Ⅱ)若b=3,sinC=2sinA,求△ABC的面积.
考点:正弦定理
专题:解三角形
分析:(Ⅰ)在△ABC中,由 bsinA=
acosB,利用正弦定理求得tanB的值,可得B的值.
(Ⅱ)由条件利用正弦定理得c=2a,再由余弦定理b2=a2+c2-2ac•cosB,求得a的值,可得c=2a的值,根据
△ABC的面积为
ac•sinB,计算求得结果.
| 3 |
(Ⅱ)由条件利用正弦定理得c=2a,再由余弦定理b2=a2+c2-2ac•cosB,求得a的值,可得c=2a的值,根据
△ABC的面积为
| 1 |
| 2 |
解答:
解:(Ⅰ)在△ABC中,∵bsinA=
acosB,
∴由正弦定理可得 sinBsinA=
sinAcosB.
∵sinA≠0,∴sinB=
cosB,∴tanB=
,∴B=
.
(Ⅱ)∵sinC=2sinA,∴c=2a,
由余弦定理b2=a2+c2-2ac•cosB,即9=a2+4a2-2a•2a•cos
,
解得a=
,c=2a=2
.
故△ABC的面积为
ac•sinB=
.
| 3 |
∴由正弦定理可得 sinBsinA=
| 3 |
∵sinA≠0,∴sinB=
| 3 |
| 3 |
| π |
| 3 |
(Ⅱ)∵sinC=2sinA,∴c=2a,
由余弦定理b2=a2+c2-2ac•cosB,即9=a2+4a2-2a•2a•cos
| π |
| 3 |
解得a=
| 3 |
| 3 |
故△ABC的面积为
| 1 |
| 2 |
3
| ||
| 2 |
点评:本题主要考查正弦定理、余弦定理的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目
函数f(x)=lnx2( )
| A、是偶函数且在(-∞,0)上单调递增 |
| B、是偶函数且在(0,+∞)上单调递增 |
| C、是奇函数且在(0,+∞)上单调递减 |
| D、是奇函数且在(-∞,0)上单调递减 |
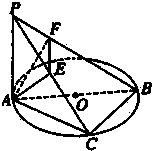 如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是
如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是