题目内容
已知等差数列{an}是递增数列,且不等式x2-6x+8<0的解集为{x|a2<x<a4}.
(1)求数列{an}的通项公式;
(2)若bn=
,求数列{bn}的前项的和Sn.
(1)求数列{an}的通项公式;
(2)若bn=
| 1 |
| anan+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件利用不等式知识求出a2=2,a4=4,再由等差数列的通项公式能求出an.
(2)由(1)推导出bn=
=
-
,由此利用裂项求和法能求出数列{bn}的前项的和Sn.
(2)由(1)推导出bn=
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(1)∵不等式x2-6x+8<0的解集为{x|2<x<4}…(2分)
且等差数列{an}是递增数列
∴a2=2,a4=4,…(4分)
∴
,
解得a1=1,d=1,
∴等差数列{an}的首项a1=1,公差d=1,…(6分)
∴an=n…(7分)
(2)∵an=n,b n=
,
∴bn=
=
-
,…(10分)
∴Sn=(1-
)+(
-
)+…+(
-
)
=1-
=
.…(13分)
且等差数列{an}是递增数列
∴a2=2,a4=4,…(4分)
∴
|
解得a1=1,d=1,
∴等差数列{an}的首项a1=1,公差d=1,…(6分)
∴an=n…(7分)
(2)∵an=n,b n=
| 1 |
| anan+1 |
∴bn=
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
点评:本题考查数列的通项公式的求法,考查前n项和公式的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
下列说法错误的是( )
| A、用平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台 |
| B、有两个面平行,其余各个面都是梯形的几何体一定都是棱台 |
| C、圆锥的轴截面是等腰三角形 |
| D、用一个平面去截球,截面是圆 |
在△ABC中,角A、B、C的对边分别是a、b、c.若asinA+csinC-
asinC=bsinB.则角B等于( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|

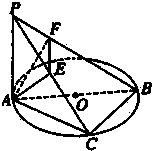 如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是
如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是