题目内容
命题:“若(x-3)2+y2≠0,则x≠3”是 命题(填真、假).
考点:命题的真假判断与应用
专题:简易逻辑
分析:先求出原命题的逆否命题,判断其真假,即可得出原命题的真假.
解答:
解:命题:“若(x-3)2+y2≠0,则x≠3”的逆否命题是“若x=3,则(x-3)2+y2=0”.
当x=3,y≠0时,(x-3)2+y2≠0,因此是假命题,可得原命题也是假命题.
故答案为:假.
当x=3,y≠0时,(x-3)2+y2≠0,因此是假命题,可得原命题也是假命题.
故答案为:假.
点评:本题考查了通过判断原命题的逆否命题的真假来判断原命题的真假,属于基础题.

练习册系列答案
相关题目
如图,在半径为R的圆C中,已知弦AB的长为5,则
•
=( )
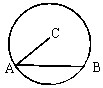
| AB |
| AC |

A、
| ||
B、
| ||
C、
| ||
D、
|
设复数z=
,则复数z2的实部与虚部的和为( )
| 2i |
| -1+i |
| A、0 | B、2 | C、-2 | D、4 |
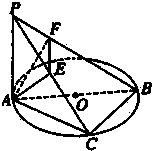 如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是
如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是