题目内容
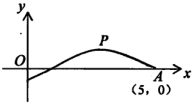 如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为
如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由函数的最值求出A,由周期求出ω,由特殊点的坐标求得φ,从而得到函数的解析式.
解答:
解:如图,根据P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,
可得A=1,
•
=5-3,求得ω=
.
再把点A(5,0)代入函数的解析式可得 sin(
×5+φ)=0,结合-π<φ<π,可得 φ=-
,
故函数的解析式为 y=sin(
x-
),
故答案为:y=sin(
x-
).
可得A=1,
| 1 |
| 4 |
| 2π |
| ω |
| π |
| 4 |
再把点A(5,0)代入函数的解析式可得 sin(
| π |
| 4 |
| π |
| 4 |
故函数的解析式为 y=sin(
| π |
| 4 |
| π |
| 4 |
故答案为:y=sin(
| π |
| 4 |
| π |
| 4 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由特殊点的坐标求得φ,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
下列说法错误的是( )
| A、用平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台 |
| B、有两个面平行,其余各个面都是梯形的几何体一定都是棱台 |
| C、圆锥的轴截面是等腰三角形 |
| D、用一个平面去截球,截面是圆 |
在△ABC中,角A、B、C的对边分别是a、b、c.若asinA+csinC-
asinC=bsinB.则角B等于( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
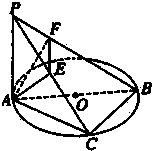 如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是
如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是