题目内容
已知f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a-1,2a],则y=f(x)的值域为 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:据二次函数是偶函数时:不含奇次项,偶函数的定义域关于原点对称,列出方程求出a、b,求出f(x)的解析式和定义域,利用二次函数的性质求出二函数的值域.
解答:
解:∵f(x)=ax2+bx+3a+b为偶函数,
∴b=0,且a-1+2a=0
解得b=0,a=
,
∴f(x)=
x2+1,定义域为[-
,
]
由二次函数的性质知,当x=0时,有最小值1,
当x=-
或
时,有最大值f(
)=
×(
)2+1=
,
∴f(x)的值域为[1,
]
故答案为:[1,
].
∴b=0,且a-1+2a=0
解得b=0,a=
| 1 |
| 3 |
∴f(x)=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
由二次函数的性质知,当x=0时,有最小值1,
当x=-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 31 |
| 27 |
∴f(x)的值域为[1,
| 31 |
| 27 |
故答案为:[1,
| 31 |
| 27 |
点评:本题考查了二次函数是偶函数的性质,及二次函数的单调性应用,关键是掌握二次函数是偶函数的充要条件,以及定义域关于原点对称是函数具有奇偶性的必要条件.

练习册系列答案
相关题目
设α、β是两个不重合的平面,m、n是两条不重合的直线,则以下结论错误的是( )
| A、若α∥β,m?α,则 m∥β |
| B、若m∥α,m∥β,α∩β=n,则 m∥n |
| C、若m?α,n?α,m∥β,n∥β,则α∥β |
| D、若m∥α,m⊥β,则α⊥β |

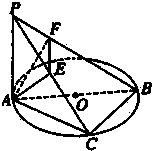 如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是
如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是