题目内容
复平面内有A，B，C三点，点A对应的复数为2+i，向量
对应的复数为2+3i，向量
对应的复数为3-i，则点C对应的复数 ．
| BA |
| BC |
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：利用复数与向量的对应关系及其向量的坐标运算即可得出．
解答：
解：设C（x，y），（x，y∈R）．
∵
=
-
=（3，-1）-（2，3）=（1，-4），
∴（x，y）-（2，1）=（1，-4），
化为（x，y）=（2，1）+（1，-4）=（3，-3），∴x=3，y=-3．
∴点C对应的复数是3-3i．
故答案为：3-3i．
∵
| AC |
| BC |
| BA |
∴（x，y）-（2，1）=（1，-4），
化为（x，y）=（2，1）+（1，-4）=（3，-3），∴x=3，y=-3．
∴点C对应的复数是3-3i．
故答案为：3-3i．
点评：本题考查了复数与向量的对应关系及其向量的坐标运算，属于基础题．
练习册系列答案
相关题目
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，对人体健康和大气环境质量的影响很大．我国PM2.5标准采用世卫组织设定的最宽限值，即PM2.5日均值在35微克/立方以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．某市环保局从360天的市区PM2.5监测数据中，随机抽取15天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）．如图，在半径为R的圆C中，已知弦AB的长为5，则
•
=（ ）
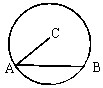
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法错误的是（ ）
| A、用平行于棱锥底面的平面去截棱锥，底面与截面之间的部分，这样的多面体叫做棱台 |
| B、有两个面平行，其余各个面都是梯形的几何体一定都是棱台 |
| C、圆锥的轴截面是等腰三角形 |
| D、用一个平面去截球，截面是圆 |
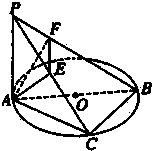如图，PA⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，AE⊥PC，AF⊥PB，给出下列结论：①AE⊥BC；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC，其中真命题的序号是