题目内容
已知a>0且a≠1,函数f(x)=ax-x.
(1)求函数y=f(x)的极值点;
(2)对x∈R使f(x)≥0恒成立,求a的取值范围.
(1)求函数y=f(x)的极值点;
(2)对x∈R使f(x)≥0恒成立,求a的取值范围.
考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:计算题,分类讨论,导数的综合应用,不等式的解法及应用
分析:(1)求出导数,讨论0<a<1,a>1,求得单调性,进而确定极值;
(2)分析0<a<1时,ax≥x在R上不可能恒成立,则a>1,由(1)可得,f(x)在x=x0处取得极小值,且为最小值,对x∈R使f(x)≥0恒成立,则f(x0)≥0,解不等式即可得到a的范围.
(2)分析0<a<1时,ax≥x在R上不可能恒成立,则a>1,由(1)可得,f(x)在x=x0处取得极小值,且为最小值,对x∈R使f(x)≥0恒成立,则f(x0)≥0,解不等式即可得到a的范围.
解答:
解:(1)函数f(x)=ax-x的导数为f′(x)=axlna-1=lna(ax-
),
当0<a<1时,f′(x)<0,f(x)在R上递减,无极值点;
当a>1时,由ax=
,得x=-
,f′(x)>0,可得,x>-
,
f′(x)<0,可得,x<-
,
则x0=-
为f(x)的极小值点,无极大值点;
(2)当0<a<1时,由y=ax和y=x的图象可得ax≥x在R上不可能恒成立.
则a>1.
由(1)得x0=-
,当x<x0,f′(x)<0,f(x)递减;
当x>x0,f′(x)>0,f(x)递增,则有f(x)在x=x0处取得极小值,且为最小值.
对x∈R使f(x)≥0恒成立,则f(x0)≥0,则
≥-
,
即有ln(lna)≥-1,即lna≥
,解得,a≥e
.
则当a≥e
时,f(x)≥0对x∈R恒成立.
| 1 |
| lna |
当0<a<1时,f′(x)<0,f(x)在R上递减,无极值点;
当a>1时,由ax=
| 1 |
| lna |
| ln(lna) |
| lna |
| ln(lna) |
| lna |
f′(x)<0,可得,x<-
| ln(lna) |
| lna |
则x0=-
| ln(lna) |
| lna |
(2)当0<a<1时,由y=ax和y=x的图象可得ax≥x在R上不可能恒成立.
则a>1.
由(1)得x0=-
| ln(lna) |
| lna |
当x>x0,f′(x)>0,f(x)递增,则有f(x)在x=x0处取得极小值,且为最小值.
对x∈R使f(x)≥0恒成立,则f(x0)≥0,则
| 1 |
| lna |
| ln(lna) |
| lna |
即有ln(lna)≥-1,即lna≥
| 1 |
| e |
| 1 |
| e |
则当a≥e
| 1 |
| e |
点评:本题考查导数的运用:求单调区间和求极值、最值,考查不等式的恒成立问题转化为求函数最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
下面关于几何体的描述,你认为正确的是( )
| A、有一个面是多边形,其余面是三角形,由这些面围成的几何体是棱锥 |
| B、四面体的任何一个面都是三角形,都可以作为棱锥的底面 |
| C、底面是矩形的棱柱就是长方体 |
| D、底面是正方形,侧棱长等于底面边长的几何体是正方体 |
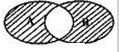 如图所示的韦恩图中,A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=
如图所示的韦恩图中,A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=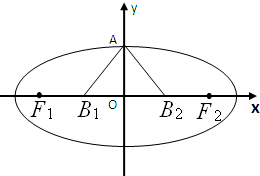 如图,设椭圆C:
如图,设椭圆C: