题目内容
下面关于几何体的描述，你认为正确的是（ ）
| A、有一个面是多边形，其余面是三角形，由这些面围成的几何体是棱锥 |
| B、四面体的任何一个面都是三角形，都可以作为棱锥的底面 |
| C、底面是矩形的棱柱就是长方体 |
| D、底面是正方形，侧棱长等于底面边长的几何体是正方体 |
考点：命题的真假判断与应用,棱柱的结构特征,棱锥的结构特征
专题：简易逻辑
分析：利用棱锥的定义判断A的正误；四面体的特征判断B的正误；长方体的特征判断C的正误；中档题的特征判断D的正误，
解答：
解：有一个面是多边形，其余面是三角形，由这些面围成的几何体是棱锥，不满足棱锥的定义，所以A不正确；
四面体的任何一个面都是三角形，都可以作为棱锥的底面，满足四面体的特征，所以B正确；
底面是矩形的棱柱不一定是长方体，侧棱垂直判断时是长方体，所以C不正确；
底面是正方形，侧棱长等于底面边长并且侧棱与底面垂直时，几何体是正方体，所以D不正确．
故选：B．
四面体的任何一个面都是三角形，都可以作为棱锥的底面，满足四面体的特征，所以B正确；
底面是矩形的棱柱不一定是长方体，侧棱垂直判断时是长方体，所以C不正确；
底面是正方形，侧棱长等于底面边长并且侧棱与底面垂直时，几何体是正方体，所以D不正确．
故选：B．
点评：本题考查空间几何体的判断与应用，掌握几何体的结构特征是解答本题的关键．
练习册系列答案
相关题目
设i是虚数单位，若复数x满足x（1-i）=i，则其虚部为（ ）
A、
| ||
B、-
| ||
C、-
| ||
D、
|
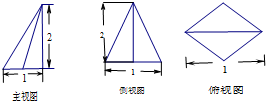一个几何体的三视图及部分数据如图所示，侧视图为等腰三角形，俯视图为正方形，则这个几何体的体积为（ ）A、
| ||
B、
| ||
| C、1 | ||
D、
|
已知S={α|α=k•90°（k∈z）}下列集合与S相等的是（ ）
| A、{α|α=90°+k•180°（k∈z）} |
| B、{α|α=90°+k•360°（k∈z）} |
| C、{α|α=±90°+k•360°（k∈z）} |
| D、{α|α=k•180°或α=90°+k•180°（k∈z）} |