题目内容
已知函数f(x)=
,则不等式f(f(x))≤3的解集为 .
|
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:函数f(x)=
,是一个分段函数,故可以将不等式f(f(x))≤3分类讨论,分x≥0,-2<x<0,x≤-2三种情况,分别进行讨论,综合讨论结果,即可得到答案.
|
解答:
解:当x≥0时,f(f(x))=f(-x2)=(-x2)2-2x2≤3,即(x2-3)(x2+1)≤0,解得0≤x≤
,
当-2<x<0时,f(f(x))=f(x2+2x)=(x2+2x)2+2(x2+2x)≤3,即(x2+2x-1)(x2+2x+3)≤0,解得-2<x<0,
当x≤-2时,f(f(x))=f(x2+2x)=-(x2+2x)2≤3,解得x≤-2,
综上所述不等式的解集为(-∞,
]
故答案为:(-∞,
]
| 3 |
当-2<x<0时,f(f(x))=f(x2+2x)=(x2+2x)2+2(x2+2x)≤3,即(x2+2x-1)(x2+2x+3)≤0,解得-2<x<0,
当x≤-2时,f(f(x))=f(x2+2x)=-(x2+2x)2≤3,解得x≤-2,
综上所述不等式的解集为(-∞,
| 3 |
故答案为:(-∞,
| 3 |
点评:本题考查的知识点是分段函数的解析式,及不等式的解法,其中根据分段函数分段处理的原则,需要进行分类讨论,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
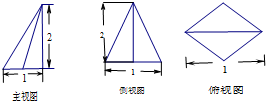 一个几何体的三视图及部分数据如图所示,侧视图为等腰三角形,俯视图为正方形,则这个几何体的体积为( )
一个几何体的三视图及部分数据如图所示,侧视图为等腰三角形,俯视图为正方形,则这个几何体的体积为( )A、
| ||
B、
| ||
| C、1 | ||
D、
|