题目内容
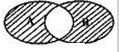如图所示的韦恩图中，A，B是非空集合，定义集合A*B为阴影部分表示的集合，若x，y∈R，A={x|y=log
|
| x+1 |
| 1-2x |
考点：对数函数的单调性与特殊点,Venn图表达集合的关系及运算
专题：集合
分析：分析求出集合A，B，进而根据A#B={x|x∈A，或x∈B，且x∉A∩B}，得到答案．
解答：
解：∵A={x|y=
}，
∴
解得0≤x＜1，
∴A=[0，1），
∵B={x|
≤1}，
∴B=（-∞，0]∪（
，+∞）
故A*B={x|x∈A，或x∈B，且x∉A∩B}=（-∞，0）∪（0，
]∪（1，+∞），
故答案为：（-∞，0）∪（0，
]∪（1，+∞）
log
|
∴
|
解得0≤x＜1，
∴A=[0，1），
∵B={x|
| x+1 |
| 1-2x |
∴B=（-∞，0]∪（
| 1 |
| 2 |
故A*B={x|x∈A，或x∈B，且x∉A∩B}=（-∞，0）∪（0，
| 1 |
| 2 |
故答案为：（-∞，0）∪（0，
| 1 |
| 2 |
点评：本小题考查数形结合的思想，考查集合交并运算的知识，属于基础题．
练习册系列答案
相关题目
下列命题中，是真命题的是（ ）
| A、平面内与两定点距离之和为常数的点的轨迹是椭圆 |
| B、平面内与两定点距离之差绝对值为常数的点的轨迹是双曲线 |
| C、平面内到点A（0，3）和到定直线y=-6距离相等的点的轨迹是抛物线 |
| D、一个命题的否命题为真，则它本身一定为假 |