题目内容
已知函数f(x)=
,g(x)=ax+1(a>0),对任意的x2∈[-1,1],总存在x1∈[π,
],使f(x1)=g(x2),则实数a的取值范围是 .
| (1+sinx)(3+sinx) |
| 2+sinx |
| 3π |
| 2 |
考点:三角函数的最值
专题:函数的性质及应用,三角函数的图像与性质
分析:由任意的x2∈[-1,1],总存在x1∈[π,
],使f(x1)=g(x2),可得g(x)=ax+1在x2∈[-1,1]的值域为f(x)在x1∈[π,
]的值域的子集,构造关于a的不等式组,可得结论.
| 3π |
| 2 |
| 3π |
| 2 |
解答:
解:当x1∈[π,
]时,sinx∈[-1,0],
令t=sinx,则y=f(x)=
=
=t+2-
,
由y=t+2-
在[-1,0]上为增函数,
故y∈[0,
],
任意的x2∈[-1,1],总存在x1∈[π,
],使f(x1)=g(x2),
∴当x2∈[-1,1]时,g(x2)⊆[0,
]
∵a>0,
∴
,解得0<a≤
,
∴实数a的取值范围是(0,
]
故答案为:(0,
]
| 3π |
| 2 |
令t=sinx,则y=f(x)=
| (1+sinx)(3+sinx) |
| 2+sinx |
| (1+t)(3+t) |
| 2+t |
| 1 |
| t+2 |
由y=t+2-
| 1 |
| t+2 |
故y∈[0,
| 3 |
| 2 |
任意的x2∈[-1,1],总存在x1∈[π,
| 3π |
| 2 |
∴当x2∈[-1,1]时,g(x2)⊆[0,
| 3 |
| 2 |
∵a>0,
∴
|
| 1 |
| 2 |
∴实数a的取值范围是(0,
| 1 |
| 2 |
故答案为:(0,
| 1 |
| 2 |
点评:本题考查的知识点是二次函数在闭区间上的最值,其中根据已知分析出“g(x)=ax+1在x2∈[-1,1]的值域为f(x)在x1∈[π,
]的值域的子集”是解答的关键.
| 3π |
| 2 |

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 已知底面是边长为2的正三角形的三棱柱,其正视图(如图所示的矩形)的面积为8,则侧视图的面积为
已知底面是边长为2的正三角形的三棱柱,其正视图(如图所示的矩形)的面积为8,则侧视图的面积为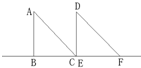 如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )
如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )


