题目内容
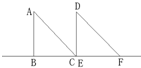 如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )
如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )A、 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:根据条件建立函数关系,求出三角形的面积,即可得到结论.
解答:
 解:设等腰直角三角形的直角边长为1,当0≤x≤1时,三角形CEG的面积y=
解:设等腰直角三角形的直角边长为1,当0≤x≤1时,三角形CEG的面积y=
EC•GE=
x2为抛物线,
当1<x≤2时, 重合的部分为△FBG,此时EC=x,BE=x-1,BF=1-(x-1)=2-x,
重合的部分为△FBG,此时EC=x,BE=x-1,BF=1-(x-1)=2-x,
对应的面积y=
(2-x)2,x>1.
故对应的图象为C,
故选:C
 解:设等腰直角三角形的直角边长为1,当0≤x≤1时,三角形CEG的面积y=
解:设等腰直角三角形的直角边长为1,当0≤x≤1时,三角形CEG的面积y=| 1 |
| 2 |
| 1 |
| 2 |
当1<x≤2时,
 重合的部分为△FBG,此时EC=x,BE=x-1,BF=1-(x-1)=2-x,
重合的部分为△FBG,此时EC=x,BE=x-1,BF=1-(x-1)=2-x,对应的面积y=
| 1 |
| 2 |
故对应的图象为C,

故选:C
点评:本题主要考查函数图象的识别和判断,根据条件建立函数关系是解决本题的关键.

练习册系列答案
相关题目
已知函数f(x)=
,g(x)=ax+1(a>0),对任意的x2∈[-1,1],总存在x1∈[π,
],使f(x1)=g(x2),则实数a的取值范围是 .
| (1+sinx)(3+sinx) |
| 2+sinx |
| 3π |
| 2 |
如图,□ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD于E,若DE=2AB,则∠AED的大小是( )


| A、60° | B、65° |
| C、70° | D、75° |
一个底面半径为5cm,母线长为16cm的圆锥,它的侧面展开图的面积是( )
| A、80πcm2 |
| B、40πcm2 |
| C、80cm2 |
| D、40cm2 |
设全集U=R,A={x|x2+3x<0},B={x|x<-1},则图中阴影部分表示的集合为( )


| A、{x|-1<x<0} |
| B、{x|-1≤x<0} |
| C、{x|0<x<3} |
| D、{x|-3<x≤-1} |
设M=
+
+
+…+
,则下列正确的是( )
| 1 | ||
1+
|
| 1 | ||||
|
| 1 | ||
|
| 1 | ||||
|
| A、42<M<43 |
| B、43<M<44 |
| C、44<M<45 |
| D、45<M<46 |
设Sn为等比数列{an}的前n项和,已知3S3=a4-2,3S2=a3-2,则公比q=( )
| A、3 | B、4 | C、5 | D、6 |
下列命题中正确的是( )
| A、由五个平面围成的多面体只能是四棱锥 |
| B、圆柱、圆锥、圆台的底面都是圆 |
| C、仅有一组对面平行的六面体是棱台 |
| D、有一个面是多边形,其余各面是三角形的几何体是棱锥 |