题目内容
偶函数f(x)=ex+ae-x(e为自然对数的底数)在(0,+∞)上( )
| A、有最大值 | B、有最小值 |
| C、单调递增 | D、不单调 |
考点:指数函数综合题
专题:函数的性质及应用
分析:由题意可得 f(-x)=f(x),化简可得(a-1)ex=(a-1)e-x,解得a的值,可得f(x)=ex+e-x ,根据导数的符号可得f(x)在(0,+∞)上单调递增.
解答:
解:由于数f(x)=ex+ae-x 为偶函数,∴f(-x)=f(x),即 e-x+a•ex=ex+a•e-x,
∴(a-1)ex=(a-1)e-x,即(a-1)(ex-e-x)=0对任意的实数恒成立,
∴只有a-1=0,解得a=1,∴f(x)=ex+e-x ,
令f′(x)=ex-e-x=0,求得x=0,在(0,+∞)上,f′(x)>0,故函数单调递增,
故选:C.
∴(a-1)ex=(a-1)e-x,即(a-1)(ex-e-x)=0对任意的实数恒成立,
∴只有a-1=0,解得a=1,∴f(x)=ex+e-x ,
令f′(x)=ex-e-x=0,求得x=0,在(0,+∞)上,f′(x)>0,故函数单调递增,
故选:C.
点评:本题主要考查函数的奇偶性,函数的单调性的判断,属于中档题.

练习册系列答案
相关题目
关于x的一元二次不等式ax2-5x-50>0的解集为(x1,x2),且x2-x1=15,则a=( )
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
已知恒过定点(1,1)的圆C截直线x=-1所得弦长为2,则圆心C的轨迹方程为( )
| A、x2=4x+2y |
| B、x2=4y+2x |
| C、y2=4y+2x |
| D、y2=4x+2y |
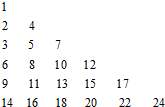 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=