题目内容
已知恒过定点（1，1）的圆C截直线x=-1所得弦长为2，则圆心C的轨迹方程为（ ）
| A、x2=4x+2y |
| B、x2=4y+2x |
| C、y2=4y+2x |
| D、y2=4x+2y |
考点：轨迹方程
专题：直线与圆,圆锥曲线的定义、性质与方程
分析：设出圆心坐标，利用勾股定理及两点间的距离公式建立方程，化简即可得出结论．
解答：
解：设C（x，y），则
∵恒过定点（1，1）的圆C截直线x=-1所得弦长为2，
∴
=
，
化简可得y2=4x+2y．
故选D．
∵恒过定点（1，1）的圆C截直线x=-1所得弦长为2，
∴
| (x+1)2+1 |
| (x-1)2+(y-1)2 |
化简可得y2=4x+2y．
故选D．
点评：本题考查轨迹方程，考查勾股定理及两点间的距离公式，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
若点（a，-1）在函数y=log
x的图象上，则tan
的值为（ ）
| 1 |
| 2 |
| aπ |
| 6 |
| A、0 | ||||
B、
| ||||
| C、1 | ||||
D、
|
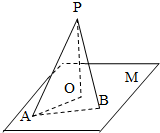如图，直线PO⊥平面M，垂足为O，直线PA是平面M的一条斜线，斜足为A，其中∠APO=α，过点P的动直线PB交平面M于点B，∠APB=β，则下列说法正确的是
（1）偶函数f（x）=ex+ae-x（e为自然对数的底数）在（0，+∞）上（ ）
| A、有最大值 | B、有最小值 |
| C、单调递增 | D、不单调 |
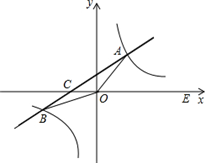如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数y=函数f(x)=log2(4x-x2)的单调递减区间是（ ）
| A、（0，4） |
| B、（0，2] |
| C、[2，4） |
| D、（2，+∞） |