关于x的一元二次不等式ax2-5x-50＞0的解集为(x1.x2).且x2-x1=15.则a=( ) A.-1B.1C.-19D.19 题目和参考答案——青夏教育精英家教网—

题目内容

关于x的一元二次不等式ax²-5x-50＞0的解集为（x₁，x₂），且x₂-x₁=15，则a=（　　）

A、-1

B、1

C、-

D、

考点：一元二次方程的根的分布与系数的关系

专题：不等式的解法及应用

分析：根据关于x的一元二次不等式ax²-5x-50＞0的解集为（x₁，x₂），可得a＜0，且x₂=

5-5

1+8a

，x₁=

5+5

1+8a

，结合x₂-x₁=15，即可求出a的值．

解答： 解：∵关于x的一元二次不等式ax²-5x-50＞0的解集为（x₁，x₂），
∴a＜0，且x₂=

5-5

1+8a

，x₁=

5+5

1+8a

，
∵x₂-x₁=15，
∴

-10

1+8a

=15，
∴a=-

．
故选C．

点评：本题考查不等式的解法，考查不等式的解集与方程解的关系，考查学生的计算能力，属于中档题．

练习册系列答案

相关题目

A、17	B、-11
C、11	D、-17

已知函数f（x）=x²+bx+2，当x∈[-1，4]时，f（x）≥b+3恒成立，则b=

．

已知⊙M：x²+（y-2）²=1，Q是x轴上的动点，QA，QB分别切⊙M于A，B两点．
（1）若|AB|=

，求|MQ|、Q点的坐标以及直线MQ的方程；
（2）求证：直线AB恒过定点．

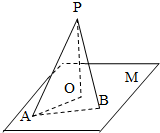如图，直线PO⊥平面M，垂足为O，直线PA是平面M的一条斜线，斜足为A，其中∠APO=α，过点P的动直线PB交平面M于点B，∠APB=β，则下列说法正确的是

①若α=0°，β=90°，则动点B的轨迹是一个圆；
②若α≠0°，β=90°，则动点B的轨迹是一条直线；
③若α≠0°，β≠90°且α+β=90°，则动点B的轨迹是抛物线；
④α≠0°，β≠90°且α+β＞90°，则动点B的轨迹是椭圆；
⑤α≠0°，β≠90°且α+β＜90°，则动点B的轨迹是双曲线．

已知a=（sin2x，2cos²x-1），b=（sinθ，cosθ）（0＜θ＜π），函数f（x）=a•b的图象经过点（

，1）．
（Ⅰ）求θ及f（x）的最小正周期；
（Ⅱ）当x∈[-

．
（2）已知函数f（x）=-x³+ax²+bx（a，b∈R）的图象如右图所示，它与x轴在原点处相切，且x轴与函数图象所围区域（图中阴影部分）的面积为

，则a的值为

．

偶函数f（x）=e^x+ae^-x（e为自然对数的底数）在（0，+∞）上（　　）

A、有最大值	B、有最小值
C、单调递增	D、不单调

不等式：

x+1	1
-1	x

≤1的解集是

．

试题分类