题目内容
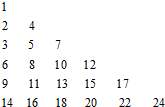 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=考点:归纳推理
专题:规律型
分析:通过观察给出的三角形数表,找到如下规律,奇数行都是奇数,偶数行都是偶数,且每一行的数的个数就是行数,然后根据2013是第1007个奇数,利用等差数列的前n项和公式分析出它所在的行数,再利用等差数列的通项公式求其所在的列数,则i与j的和可求.
解答:
解:由三角形数表可以看出其奇数行中的数都是奇数,偶数行中的数都是偶数,2013=2×1007-1,
∴2013为第1007个奇数,又每一行中奇数的个数就是行数,又前31个奇数行内奇数的个数的和为31×1+
=961,
即第31个奇数行的最后一个奇数是961×2-1=1921,前32个奇数行内奇数的个数的和为32×1+
=1024,
故2013在第32个奇数行内,
∴i=63,
∵第63行的第一个数为1923,
则2013=1923+2(m-1),
∴m=46,
即j=46,
∴i+j=63+46=109.
故答案为:109.
∴2013为第1007个奇数,又每一行中奇数的个数就是行数,又前31个奇数行内奇数的个数的和为31×1+
| 31(31-1)×2 |
| 2 |
即第31个奇数行的最后一个奇数是961×2-1=1921,前32个奇数行内奇数的个数的和为32×1+
| 32(32-1)×2 |
| 2 |
故2013在第32个奇数行内,
∴i=63,
∵第63行的第一个数为1923,
则2013=1923+2(m-1),
∴m=46,
即j=46,
∴i+j=63+46=109.
故答案为:109.
点评:本题考查简单的归纳推理的应用,根据数表中的数值归纳出数的特点是解决本题的关键,考查学生的归纳能力.

练习册系列答案
相关题目
用秦九韶算法求多项式f(x)=5x5+4x4+3x3+2x2+x+1,当x=2时的值的过程中,不会出现的数值为( )
| A、14 | B、127 |
| C、259 | D、64 |
偶函数f(x)=ex+ae-x(e为自然对数的底数)在(0,+∞)上( )
| A、有最大值 | B、有最小值 |
| C、单调递增 | D、不单调 |
已知△ABC中,a=6,b=7,c=8,则△ABC一定是( )
| A、无法确定 | B、直角三角形 |
| C、锐角三角形 | D、钝角三角形 |
在△ABC中,已知∠A=120°,且
=
,则sinC等于( )
| AC |
| AB |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 (1)
(1)