题目内容
14.已知函数f(x)是奇函数,且满足f(2-x)=f(x)(x∈R),当0<x≤1时,f(x)=lnx+2,则函数y=f(x)在(-2,4]上的零点个数是( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 由函数f(x)是奇函数且满足f(2-x)=f(x)知,f(x)是周期为4的周期函数,且关于直线x=1+2k(k∈R)成轴对称,关于点(2k,0)(k∈Z)成中心对称,再求出函数的零点,即可得出结论.
解答 解:由函数f(x)是奇函数且满足f(2-x)=f(x)知,f(x)是周期为4的周期函数,
且关于直线x=1+2k(k∈Z)成轴对称,关于点(2k,0)(k∈Z)成中心对称.
当0<x≤1时,令f(x)=lnx+2=0,得$x=\frac{1}{e^2}$,由此得y=f(x)在(-2,4]上的零点分别为$-2+\frac{1}{e^2},-\frac{1}{e^2},0,\frac{1}{e^2},2-\frac{1}{e^2},2,2+\frac{1}{e^2},-\frac{1}{e^2}+4,4$共9个零点.
故选C.
点评 淘宝同款车函数的奇偶性、对称性,考查函数的零点,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
2.已知函数y=2|x|-4的图象与曲线C:x2+λy2=4恰有两个不同的公共点,则实数λ的取值范围是( )
| A. | [-$\frac{1}{4}$,$\frac{1}{4}$) | B. | [-$\frac{1}{4}$,$\frac{1}{4}$] | C. | (-∞,-$\frac{1}{4}$]∪(0,$\frac{1}{4}$) | D. | (-∞,-$\frac{1}{4}$]∪[$\frac{1}{4}$,+∞) |
9.已知函数$f(x)=\frac{alnx}{x}({a∈R})$的图象与直线x-2y=0相切,当函数g(x)=f(f(x))-t恰有一个零点时,实数t的取值范围是( )
| A. | {0} | B. | [0,1] | C. | [0,1) | D. | (-∞,0) |
6.已知抛物线E的焦点为F,准线为l,过F的直线m与E交于A,B两点,C,D分别为A,B在l上的射影,M为AB的中点,若m与l不平行,则△CMD是( )
| A. | 等腰三角形且为锐角三角形 | B. | 等腰三角形且为钝角三角形 | ||
| C. | 等腰直角三角形 | D. | 非等腰的直角三角形 |
4.已知函数y=cosx与y=sin(2x+φ)(0≤φ≤π),它们的图象有一个横坐标为$\frac{π}{3}$的交点,则φ=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
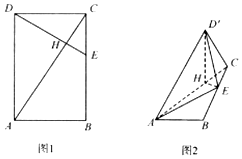 如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.
如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.