题目内容
3.在数列{an}中,a2=$\frac{2}{3}$.(1)若数列{an}满足2an-an+1=0,求an;
(2)若a4=$\frac{4}{7}$,且数列{(2n-1)an+1}是等差数列,求数列{$\frac{n}{{a}_{n}}$}的前n项和Tn.
分析 (1)由a2=$\frac{2}{3}$,2an-an+1=0,求出数列{an}的首项,并得到数列{an}是以$\frac{1}{3}$为首项,以2为公比的等比数列,由等比数列的通项公式得答案;
(2)由已知结合数列{(2n-1)an+1}是等差数列求其公差,进一步得到数列{(2n-1)an+1}的通项公式,代入{$\frac{n}{{a}_{n}}$},再由等差数列的前n项和得答案.
解答 解:(1)由a2=$\frac{2}{3}$,2an-an+1=0,得${a}_{1}=\frac{1}{3}$,且$\frac{{a}_{n+1}}{{a}_{n}}=2$.
∴数列{an}是以$\frac{1}{3}$为首项,以2为公比的等比数列,
则${a}_{n}=\frac{1}{3}•{2}^{n-1}$;
(2)∵a2=$\frac{2}{3}$,a4=$\frac{4}{7}$,且数列{(2n-1)an+1}是等差数列,
则数列{(2n-1)an+1}的公差为d=$\frac{[(2×4-1)×\frac{4}{7}+1]-[(2×2-1)×\frac{2}{3}+1]}{4-2}$=1.
∴(2n-1)an+1=(2×2-1)×$\frac{2}{3}$+1+(n-2)×1=n+1,
∴${a}_{n}=\frac{n}{2n-1}$,
则$\frac{n}{{a}_{n}}$=$\frac{n}{\frac{n}{2n-1}}=2n-1$.
∴Tn=1+3+5+…+(2n-1)=$\frac{[1+(2n-1)]×n}{2}={n}^{2}$.
点评 本题考查数列递推式,考查了等比数列通项公式的求法,考查等差数列的通项公式,属中档题.

练习册系列答案
相关题目
13.在直角梯形ABCD中,∠A=90°,AD∥BC,BC=2AD,△ABD的面积为2,若$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{EC}$,BE⊥DC,则$\overrightarrow{DA}$$•\overrightarrow{DC}$的值为( )
| A. | -2 | B. | -2$\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
8.已知函数f(x)=$\left\{\begin{array}{l}{kx+2,x≥0}\\{{(\frac{1}{2})}^{x},x<0}\end{array}\right.$,若方程f(f(x))-$\frac{3}{2}$=0在实数集范围内无解,则实数k的取值范围是( )
| A. | (-1,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,$\frac{1}{3}$) | C. | [0,+∞) | D. | (-$\frac{1}{2}$,-$\frac{1}{4}$] |
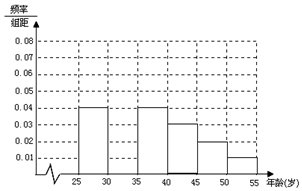 智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:
智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图: