题目内容
19.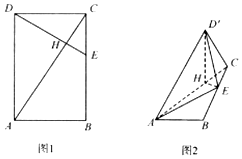 如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.
如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.(Ⅰ)求证:D'H⊥平面ABC;
(Ⅱ)求二面角H-D'E-A的余弦值.
分析 (Ⅰ)推导出AC⊥DE,DH′⊥AC,D′H⊥HE,从而D′H⊥平面ABC;
(Ⅱ)由(Ⅰ)知,HA,HE,HD'相互垂直,所以以H为坐标原点,HA,HE,HD'分别为x,y,z轴建立如图所示的空间直角坐标系H-xyz,利用向量方法,求二面角H-D'E-A的余弦值.
解答  (Ⅰ)证明:在矩形ABCD中,因为$AB=2,BC=2\sqrt{3},CE=\frac{1}{3},CB=\frac{{2\sqrt{3}}}{3}$,
(Ⅰ)证明:在矩形ABCD中,因为$AB=2,BC=2\sqrt{3},CE=\frac{1}{3},CB=\frac{{2\sqrt{3}}}{3}$,
所以$tan∠EDC=\frac{CE}{CD}=\frac{{\sqrt{3}}}{3},tan∠ACB=\frac{AB}{BC}=\frac{{\sqrt{3}}}{3}$,则∠EDC=∠ACB.
又因为$∠DCA+∠ACB=\frac{π}{2}$,所以$∠EDC+∠DCA=\frac{π}{2}$.
则$∠DHC=\frac{π}{2}$,所以AC⊥DE,即D'H⊥AC.
又△CHE∽△AHD,且$\frac{CE}{AD}=\frac{1}{3}$,所以$D'H=DH=\frac{3}{4}DE=\frac{3}{4}×\sqrt{4+\frac{4}{3}}=\frac{3}{4}×\frac{{4\sqrt{3}}}{3}=\sqrt{3}$,$HE=\frac{1}{4}DE=\frac{1}{4}×\frac{{4\sqrt{3}}}{3}=\frac{{\sqrt{3}}}{3}$.则$D'{H^2}+H{E^2}=\frac{10}{3}=D'{E^2}$,所以D'H⊥HE.
而直线AC与HE是平面ABC内的两条相交直线,所以D'H⊥平面ABC.
(Ⅱ)解:由(Ⅰ)知,HA,HE,HD'相互垂直,所以以H为坐标原点,HA,HE,HD'分别为x,y,z轴建立如图所示的空间直角坐标系H-xyz,
则$HA=\frac{1}{4}AC=\frac{3}{4}×\sqrt{4+12}=\frac{3}{4}×4=3$,$HC=\frac{1}{4}AC=\frac{1}{4}×4=1$,
所以$H({0,0,0}),A({3,0,0}),E({0,\frac{{\sqrt{3}}}{3},0}),D'({0,0,\sqrt{3}})$,$\overrightarrow{EA}=({3,-\frac{{\sqrt{3}}}{3},0}),\overrightarrow{ED}=({0,-\frac{{\sqrt{3}}}{3},\sqrt{3}})$.
设平面AED'的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{{\begin{array}{l}{3x-\frac{{\sqrt{3}}}{3}y=0}\\{-\frac{{\sqrt{3}}}{3}y+\sqrt{3}z=0}\end{array}}\right.$.取$y=\sqrt{3}$,则$x=\frac{1}{3},z=\frac{{\sqrt{3}}}{3}$,
所以$\overrightarrow{m}$=($\frac{1}{3}$,$\sqrt{3}$,$\frac{\sqrt{3}}{3}$).
又平面HD'E的一个法向量为$\overrightarrow{n}$=(1,0,0),设二面角H-D'E-A的平面角为θ,则cosθ=$\frac{\frac{1}{3}}{\sqrt{\frac{1}{9}+3+\frac{1}{3}}}$=$\frac{\sqrt{31}}{31}$,所以二面角H-D'E-A的余弦值为$\frac{{\sqrt{31}}}{31}$.
点评 本题考查线面垂直的证明,考查二面角H-D'E-A的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案| A. | (-1,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,$\frac{1}{3}$) | C. | [0,+∞) | D. | (-$\frac{1}{2}$,-$\frac{1}{4}$] |
| A. | $\frac{2}{π^2}$ | B. | $1-\frac{4}{π^2}$ | C. | $\frac{4}{π^2}$ | D. | $1-\frac{2}{π^2}$ |
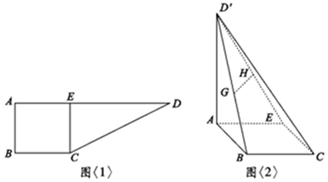 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.