题目内容
4.已知函数y=cosx与y=sin(2x+φ)(0≤φ≤π),它们的图象有一个横坐标为$\frac{π}{3}$的交点,则φ=( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 利用在$\frac{π}{3}$的函数值相等为$\frac{1}{2}$,得到φ的表达式,利用已知范围求角.
解答 解:$sin(\frac{2π}{3}+φ)=\frac{1}{2}$,$\frac{2π}{3}+φ=2kπ+\frac{π}{6}$或$2kπ+\frac{5π}{6}k∈Z$,
$φ=2kπ-\frac{π}{2}$或$2kπ+\frac{π}{6},k∈Z$,
又因为0≤φ≤π,所以$φ=\frac{π}{6}$;
故选A.
点评 本题考查了函数值的求法,关键是将问题转化为在$\frac{π}{3}$的函数值相等为$\frac{1}{2}$,求出范围内的角.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
9.在区间$[{0,\frac{π}{2}}]$上任选两个数x和y,则y<sinx的概率为( )
| A. | $\frac{2}{π^2}$ | B. | $1-\frac{4}{π^2}$ | C. | $\frac{4}{π^2}$ | D. | $1-\frac{2}{π^2}$ |
16.在区间[0,1]上任选两个数x和y,则$y≥\sqrt{1-{x^2}}$的概率为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{4}$ |
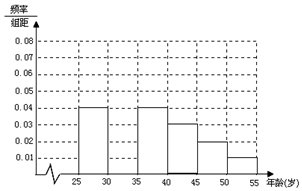 智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:
智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图: