题目内容
已知命题p：方程
+
=1表示焦点在x轴上的椭圆；命题q：方程
+
=1表示双曲线；若“p∨q”为真，“?q”为真，求实数m的取值范围．
| x2 |
| 8-2m |
| y2 |
| m-1 |
| x2 |
| 2-m |
| y2 |
| m |
考点：命题的真假判断与应用
专题：简易逻辑
分析：命题p为真时，求出1＜m＜3，命题q为真时，求出m＜0 或m＞2，然后通过复合命题的真假关系求解即可．
解答：
解：命题p为真时，椭圆为
+
=1，焦点在x轴上，
则8-2m＞m-1＞0，∴1＜m＜3．…（4分）
命题q为真时，双曲线为
+
=1
则（2-m）m＜0，∴m＜0 或m＞2．…（8分）
若“p∨q”为真，“?q”为真，则p真q假 …（11分）
则
，故1＜m≤2…（14分）
| x2 |
| 8-2m |
| y2 |
| m-1 |
则8-2m＞m-1＞0，∴1＜m＜3．…（4分）
命题q为真时，双曲线为
| x2 |
| 2-m |
| y2 |
| m |
则（2-m）m＜0，∴m＜0 或m＞2．…（8分）
若“p∨q”为真，“?q”为真，则p真q假 …（11分）
则
|
点评：本题考查命题的真假的判断与应用，圆锥曲线方程的应用，考查计算能力．
练习册系列答案
相关题目
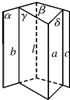求证：如果一条直线和两个相交的平面都平行，那么这条直线和它们的交线平行，已知：如图，α∩β=l，a∥α，a∥β，求证：a∥l．