题目内容
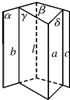求证：如果一条直线和两个相交的平面都平行，那么这条直线和它们的交线平行，已知：如图，α∩β=l，a∥α，a∥β，求证：a∥l．考点：直线与平面平行的性质
专题：空间位置关系与距离
分析：过a作平面γ交平面α于b，过a作平面ξ交平面β于C．从而b∥C，b∥β．进南昌b∥l，且a∥b．由此能证明a∥l．
解答：
证明：过a作平面γ交平面α于b，
∵a∥α，∴a∥b．同样，过a作平面ξ交平面β于C．
∵a∥β，∴a∥C．∴b∥C．
又∵b?β且C?β，∴b∥β．
又平面α经过b交β于l．
∴b∥l，且a∥b．∴a∥l．
∵a∥α，∴a∥b．同样，过a作平面ξ交平面β于C．
∵a∥β，∴a∥C．∴b∥C．
又∵b?β且C?β，∴b∥β．
又平面α经过b交β于l．
∴b∥l，且a∥b．∴a∥l．
点评：本题考查二直线平行的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
在某项测量中，测量结果ξ服从正态分布N（0，σ2）（σ＞0），若P（ξ＜-1）=0.1，则ξ在区间（0，1）内取值的概率为（ ）
| A、0.4 | B、0.5 |
| C、0.8 | D、0.9 |
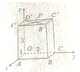如图所示，在长方形OABC-D′A′B′C′中，|OA|=1，|OC|=2，|OD′|=3，A′C′与B′D′交于点P，分别写出点C，C′，B，B′，A′，A，P的坐标．