题目内容
(2x-y)3(x+3y)2的展开式中x2y3的系数为 .
考点:二项式定理的应用
专题:二项式定理
分析:利用二项展开式的通项公式,可得结论.
解答:
解:(2x-y)3(x+3y)2的展开式中,x2y3的系数为-
•22•
•32+
•21•
•31
•20•
•30=-73.
故答案为:-73.
| C | 1 3 |
| C | 2 2 |
| C | 2 3 |
| C | 1 2 |
| -C | 3 3 |
| C | 0 2 |
故答案为:-73.
点评:二项展开式的通项公式是解决二项展开式的特定项问题的工具.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,既是单调函数又是奇函数的是( )
| A、y=log3x | ||
| B、y=3|x| | ||
C、y=x
| ||
| D、y=x3 |
在某项测量中,测量结果ξ服从正态分布N(0,σ2)(σ>0),若P(ξ<-1)=0.1,则ξ在区间(0,1)内取值的概率为( )
| A、0.4 | B、0.5 |
| C、0.8 | D、0.9 |
已知函数f(x)=
,把函数g(x)=f(x)-x的零点按照从大到小的顺序排成一个数列{an}
,则该数列的通项公式为( )
|
,则该数列的通项公式为( )
| A、an=n-1(n∈N*) |
| B、an=n(n∈N*) |
| C、an=n(n-1)(n∈N*) |
| D、an=2n-2(n∈N*) |
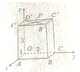 如图所示,在长方形OABC-D′A′B′C′中,|OA|=1,|OC|=2,|OD′|=3,A′C′与B′D′交于点P,分别写出点C,C′,B,B′,A′,A,P的坐标.
如图所示,在长方形OABC-D′A′B′C′中,|OA|=1,|OC|=2,|OD′|=3,A′C′与B′D′交于点P,分别写出点C,C′,B,B′,A′,A,P的坐标.