题目内容
在锐角△ABC中,a,b,c分别为角A,B,C的对边,且4sin2
-cos2A=
.
(1)求角A的大小;
(2)若BC边上高为1,求△ABC面积的最小值?
| B+C |
| 2 |
| 7 |
| 2 |
(1)求角A的大小;
(2)若BC边上高为1,求△ABC面积的最小值?
考点:三角函数中的恒等变换应用,三角函数的最值
专题:解三角形
分析:(1)利用三角形内角和,转化B+C,用诱导公式、降幂公式、倍角公式化简,得到关于cosA的方程,求得cosA,进而求得A.
(2)在Rt△ABD,Rt△ACD中,sinB=
,sinC=
,代入三角形面积公式,求得面积的最值,只需化简求表达式中分母的最值,将C用B表示,利用两角和公式化简,利用B的范围求得分母的最值,进而求得面积的最值.
(2)在Rt△ABD,Rt△ACD中,sinB=
| 1 |
| c |
| 1 |
| b |
解答:
解:(1)∵A+B+C=π,
∴sin
=sin
=cos
,
∵4sin2
-cos2A=
.
∴4cos2
-cos2A=
.
∴2(1+cosA)-(2cos2A-1)=
,
整理得(2cosA-1)2=0,
∴cosA=
,
∵0<A<π,
∴A=
.
(2)S△ABC=
bcsinA=
×
×
×
=
,
设y=4sinBsinC,
则y=4sinBsin(
-B)=2
sinBcosB+2sin2B=
sin2B+1-cos2B=2sin(2B-
)+1,
∵0<B<
,0<
-B<
,
∴
<B<
,
<2B-
<
,
∴当2B-
=
,即B=
时,y有最大值为3,
∴此时S有最小值,为
.
∴sin
| B+C |
| 2 |
| π-A |
| 2 |
| A |
| 2 |
∵4sin2
| B+C |
| 2 |
| 7 |
| 2 |
∴4cos2
| A |
| 2 |
| 7 |
| 2 |
∴2(1+cosA)-(2cos2A-1)=
| 7 |
| 2 |
整理得(2cosA-1)2=0,
∴cosA=
| 1 |
| 2 |
∵0<A<π,
∴A=
| π |
| 3 |
(2)S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| sinB |
| 1 |
| sinC |
| ||
| 2 |
| ||
| 4sinBsinC |
设y=4sinBsinC,
则y=4sinBsin(
| 2π |
| 3 |
| 3 |
| 3 |
| π |
| 6 |
∵0<B<
| π |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴当2B-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∴此时S有最小值,为
| ||
| 3 |
点评:本题主要考查了两角和与差的争先公式,二倍角公式,诱导公式,三角函数最值等基础知识.考查运用三角公式进行三角变换的能力和计算能力.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A、B两点.
如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A、B两点.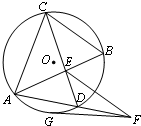 如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证:
如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证: